
【題目】某土特產公司組織20輛汽車裝運甲、乙、丙三種土特產共120噸去外地銷售.按計劃20輛車都要裝運,每輛汽車只能裝運同一種土特產,且必須裝滿,根據下表提供的信息,解答以下問題:
土特產品種 | 甲 | 乙 | 丙 |
每輛汽車運載量(噸) | 8 | 6 | 5 |
每噸土特產獲利(百元) | 12 | 16 | 10 |
(1)設裝運甲種土特產的車輛數為x,裝運乙種土特產的車輛數為y,求y與x之間的函數關系式.
(2)如果裝運每種土特產的車輛都不少于3輛,那么車輛的安排方案有幾種并寫出每種安排方案.
(3)若要使此次銷售獲利最大,應采用(2)中哪種安排方案?并求出最大利潤的值.
【答案】
(1)解:∵8x+6y+5(20﹣x﹣y)=120,
∴y=20﹣3x.
∴y與x之間的函數關系式為y=20﹣3x.
(2)解:由x≥3,y=20﹣3x≥3,即20﹣3x≥3可得3≤x≤5 ![]() ,
,
又∵x為正整數,
∴x=3,4,5.
故車輛的安排有三種方案,即:
方案一:甲種3輛乙種11輛丙種6輛;
方案二:甲種4輛乙種8輛丙種8輛;
方案三:甲種5輛乙種5輛丙種10輛
(3)解:設此次銷售利潤為W百元,
W=8x12+6(20﹣3x)16+5[20﹣x﹣(20﹣3x)]10=﹣92x+1920.
∵W隨x的增大而減小,又x=3,4,5
∴當x=3時,W最大=1644(百元)=16.44萬元.
答:要使此次銷售獲利最大,應采用(2)中方案一,即甲種3輛,乙種11輛,丙種6輛,最大利潤為16.44萬元.
【解析】(1)因為公司組織20輛汽車裝運甲、乙、丙三種土特產共120噸去外地銷售,設裝運甲種土特產的車輛數為x,裝運乙種土特產的車輛數為y,則裝運丙特產的車輛數為(20﹣x﹣y),且8x+6y+5(20﹣x﹣y)=120,整理即得y與x之間的函數關系式.(2)因為裝運每種土特產的車輛都不少于3輛,所以x≥3,y≥3,20﹣x﹣y≥3,結合(1)的答案,就可得到關于x的不等式組,又因x是正整數,從而可求x的取值,進而確定方案.(3)可設此次銷售利潤為W百元,由表格可得W=8x12+6(20﹣3x)16+5[20﹣x﹣(20﹣3x)]10=﹣92x+1920,根據y隨x的變化規律,結合(2)中所求,就可確定使利潤最大的方案.


 黃岡冠軍課課練系列答案
黃岡冠軍課課練系列答案科目:初中數學 來源: 題型:
【題目】如圖,點P是正方形ABCD內的一點,連接CP,將線段CP繞點C順時針旋轉90°,得到線段CQ,連接BP,DQ.
(1)如圖a,求證:△BCP≌△DCQ;
(2)如圖,延長BP交直線DQ于點E.
①如圖b,求證:BE⊥DQ;
②如圖c,若△BCP為等邊三角形,判斷△DEP的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1個單位長度的小正方形組成的網格中.

(1)把△ABC平移至A′的位置,使點A與A′對應,得到△A′B′C′;
(2)線段AA′與BB′的關系是: ;
(3)求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形網格中,每個小正方形的邊長為1,格點△ABC的頂點A、C的坐標分別為(﹣4,5)、(﹣1,3).
(1)請在圖中正確作出平面直角坐標系;
(2)請作出△ABC關于y軸對稱的△A′B′C′;
(3)點B′的坐標為 ,△A′B′C′的面積為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,一次函數y=﹣2x+1的圖象與y軸交于點A.
(1)若點A關于x軸的對稱點B在一次函數y= ![]() x+b的圖象上,求b的值,并在同一坐標系中畫出該一次函數的圖象;
x+b的圖象上,求b的值,并在同一坐標系中畫出該一次函數的圖象;
(2)求這兩個一次函數的圖象與y軸圍成的三角形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線l的同側有A,B,C三點,如果A,B兩點確定的直線l1與B,C兩點確定的直線l2都與l平行,那么A,B,C三點在同一條直線上,理由是________________________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正比例函數y=2x的圖象與一次函數y=kx+b的圖象交于點A(m,2),一次函數圖象經過點B(﹣2,﹣1),與y軸的交點為C,與x軸的交點為D. 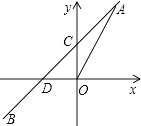
(1)求一次函數解析式;
(2)求C點的坐標;
(3)求△AOD的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com