【題目】已知∠AOB＝100°，∠BOC＝60°，OM平分∠AOB，ON平分∠BOC，求∠MON的度數．
【答案】20°或80°
【解析】
注意此題要分兩種情況：①當OC落在∠AOB的內部時，②當OC落在∠AOB的外部時；利用角的和差關系計算，
分兩種情況計算：
①當OC落在∠AOB的內部時：
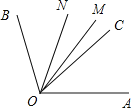
∵OM平分∠AOB，
∴∠AOM＝
∠AOB＝×100°＝50°，
∵ON平分∠BOC，
∴∠BON＝∠BOC＝×60°＝30°，
∴∠MON＝∠AOB﹣∠AOM﹣∠BON＝100°﹣50°﹣30°＝20°，
②當OC落在∠AOB的外部時；
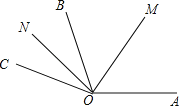
∵OM平分∠AOB，ON平分∠BOC，
∴∠BOM＝∠AOB＝×100°＝50°，
∠BON＝∠BOC＝×60°＝30°，
∴∠MON＝∠BOM+∠BON＝50°+30°＝80°
綜上所述，∠MON的度數為20°或80°．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖1所示，點O為直線AB上一點，過點O作射線OC，使
，將一塊透明的三角尺的直角頂點放在點O處，邊OM在射線OB上，邊ON在直線AB的下方.
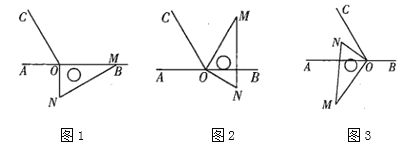
（1）將圖1中的三角尺繞點O逆時針旋轉至如圖2所示的位置，使邊OM在
的內部，且恰好平分，求
的度數.
（2）將圖1中的三角尺繞點O按每秒
的速度逆時針旋轉一周，在旋轉過程中，第t秒時，直線ON恰好平分銳角
，則t的值為________（直接寫出結果）.
（3）將圖1中的三角尺繞點O逆時針旋轉至如圖3所示的位置，使ON在的內部，請探究
與
之間的關系，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校八年級共有800名學生，準備調查他們對“低碳”知識的了解程度．
（1）在確定調查方式時，團委設計了以下三種方案：
方案一：調查八年級部分女生；
方案二：調查八年級部分男生；
方案三：到八年級每個班去隨機調查一定數量的學生．
請問其中最具有代表性的一個方案是_____；
（2）團委采用了最具有代表性的調查方案，并用收集到的數據繪制出兩幅不完整的統計圖（如圖①、圖②所示），請你根據圖中信息，將兩個統計圖補充完整；
（3）請你估計該校八年級約有多少名學生比較了解“低碳”知識．
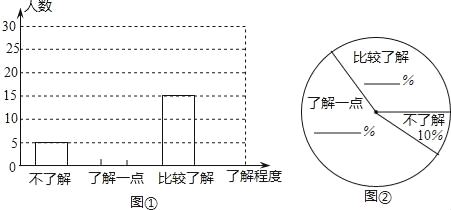
查看答案和解析>>
科目：初中數學 來源： 題型：
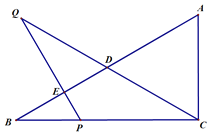
【題目】已知,如圖, 在
中, 
,
,
,P是邊BC上的一動點，過點P作PE⊥AB,垂足為E，延長PE至點Q，使PQ=PC, 聯結
交邊AB于點
.
（1）求AD的長；
（2）設
,
的面積為y, 求y關于x的函數解析式，并寫出定義域；
（3）過點C作
, 垂足為F, 聯結PF、QF, 試探索當點P在邊BC的什么位置時，
為等邊三角形？請指出點P的位置并加以證明.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】特殊兩位數乘法的速算——如果兩個兩位數的十位數字相同，個位數字相加為10，那么能立說出這兩個兩位數的乘積.如果這兩個兩位數分別寫作AB和AC（即十位數字為A，個位數字分別為B、C，B+C=10，A>3），那么它們的乘積是一個4位數，前兩位數字是A和(A+1)的乘積，后兩位數字就是B和C的乘積.
如：47×43=2021，61×69=4209.
（1）請你直接寫出83×87的值；
（2）設這兩個兩位數的十位數字為x(x>3)，個位數字分別為y和z（y+z=10)，通過計算驗證這兩個兩位數的乘積為100x(x+1)+yz.
（3）99991×99999=___________________（直接填結果）
【答案】7221
【解析】分析：
套用上面的歸納總結代入數據，即可得出結論；
利用上面總結的結論套入數據表示出該兩個兩位數的成績，在將等式展開合并同類項得出左邊=右邊，從而證明結論成立．
直接運算即可.
詳解：(1)83和87滿足題中的條件，即十位數都是8,8>3,且個位數字分別是3和7，之和為10,那么它們的乘積是一個4位數，前兩位數字是8和9的乘積，后兩位數字就是3和7的乘積，因而，答案為：7221.
(2) 這兩個兩位數的十位數字為x(x>3)，個位數字分別為y和z，則由題知y+z=10,
因而有：(10x+y)(10x+z)=100x2+10xz+10xy+yz
=100x2+10x(y+z)+yz,
=100x2+100x+yz,
=100x(x+1)+yz.
（3）9999000009.
點睛：通過閱讀題干掌握題中所給信息得出推理方法，然后通過多項式的展開式得出答案.學生應熟練掌握歸納推理的數學思想.
【題型】解答題
【結束】
19
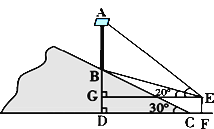
【題目】為了大力弘揚和踐行社會主義核心價值觀，某鄉鎮在一條公路旁的小山坡上，樹立一塊大型標語牌AB，如圖所示，標語牌底部B點到山腳C點的距離BC為20米，山坡的坡角為30°． 某同學在山腳的平地F處測量該標語牌的高，測得點C到測角儀EF的水平距離CF = 1.7米，同時測得標語牌頂部A點的仰角為45°，底部B點的仰角為20°，求標語牌AB的高度．（參考數值：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，
）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】解不等式組：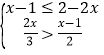
, 并把解集在數軸上表示出來.
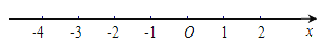
【答案】-3＜x≤1
【解析】分析：分別解不等式，在數軸上表示出解集,找出解集的公共部分即可.
詳解：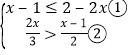
，
解不等式①得：
，
解不等式②得：
∴原不等式組的解集為-3＜x≤1
解集在數軸上表示為：
點睛：考查解一元一次不等式組，比較容易，分別解不等式，找出解集的公共部分即可.
【題型】解答題
【結束】
17
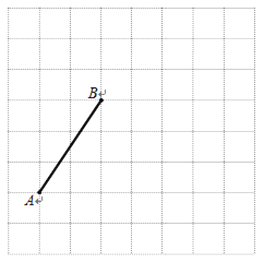
【題目】下圖是由邊長為1個單位長度的小正方形組成的網格，線段AB的端點在格點上.
（1）請建立適當的平面直角坐標系xOy，使得A點的坐標為（-3，-1），在此坐標系下，B點的坐標為________________；
（2）將線段BA繞點B逆時針旋轉90°得線段BC，畫出BC；在第(1)題的坐標系下，C點的坐標為__________________；
（3）在第(1)題的坐標系下，二次函數y=ax2+bx+c(a≠０)的圖象過O、B、C三點，則此函數圖象的對稱軸方程是________________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】列方程解應用題：
周末，小明從城里去渡假村接父母回家，為了欣賞路邊的風景，小明從城里步行出發，同時父母也從渡假村步行出發，相向而行，城里距渡假村
，小明每小時走
，父母每小時走
，如果小明帶一只狗和他同時出發，狗以每小時
的速度向父母方向跑去，遇到父母后又立即回頭跑向小明，遇到小明后又立即回頭跑向父母，這樣往返直到二人相遇.
（1）小明與父母經過多少小時相遇？
（2）這只狗共跑了多少
呢？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】【探索發現】
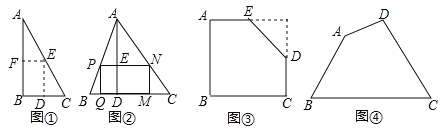
如圖①，是一張直角三角形紙片，∠B=60°，小明想從中剪出一個以∠B為內角且面積最大的矩形，經過多次操作發現，當沿著中位線DE、EF剪下時，所得的矩形的面積最大，隨后，他通過證明驗證了其正確性，并得出：矩形的最大面積與原三角形面積的比值為 ．
【拓展應用】
如圖②，在△ABC中，BC=a，BC邊上的高AD=h，矩形PQMN的頂點P、N分別在邊AB、AC上，頂點Q、M在邊BC上，則矩形PQMN面積的最大值為 ．（用含a，h的代數式表示）
【靈活應用】
如圖③，有一塊“缺角矩形”ABCDE，AB=32，BC=40，AE=20，CD=16，小明從中剪出了一個面積最大的矩形（∠B為所剪出矩形的內角），求該矩形的面積．
【實際應用】
如圖④，現有一塊四邊形的木板余料ABCD，經測量AB=50cm，BC=108cm，CD=60cm，且tanB=tanC=
，木匠徐師傅從這塊余料中裁出了頂點M、N在邊BC上且面積最大的矩形PQMN，求該矩形的面積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
