
【題目】如圖,線段AB上有一任意點C,點M是線段AC的中點,點N是線段BC的中點,當AB=6cm時,
(1)求線段MN的長.
(2)當C在AB延長線上時,其他條件不變,求線段MN的長.
![]()
【答案】(1)3cm;(2)3cm
【解析】
(1)由于點M是AC中點,所以MC=![]() AC,由于點N是BC中點,則CN=
AC,由于點N是BC中點,則CN=![]() BC,而MN=MC+CN=
BC,而MN=MC+CN=![]() (AC+BC)=
(AC+BC)=![]() AB,從而可以求出MN的長度;
AB,從而可以求出MN的長度;
(2)當C在AB延長線上時,由于點M是AC中點,所以MC=![]() AC,由于點N是BC中點,則CN=
AC,由于點N是BC中點,則CN=![]() BC,而MN=MC-CN=
BC,而MN=MC-CN=![]() (AC-BC)=
(AC-BC)=![]() AB,從而可以求出MN的長度.
AB,從而可以求出MN的長度.
解:(1)如圖:
![]()
∵點M是AC中點,點N是BC中點,
∴MC=![]() AC,CN=
AC,CN=![]() BC,
BC,
∴MN=MC+CN=![]() (AC+BC)=
(AC+BC)=![]() AB=
AB=![]() ×6=3(cm);
×6=3(cm);
(2)當C在AB延長線上時,如圖:
![]()
∵點M是AC中點,點N是BC中點,
∴MC=![]() AC,CN=
AC,CN=![]() BC,
BC,
∴MN=MC-CN=![]() (AC-BC)=
(AC-BC)=![]() AB=
AB=![]() ×6=3(cm);
×6=3(cm);


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖 1,在平面直角坐標系中,點 A 為 x 軸負半軸上一點,點 B 為 x 軸正半軸上一點,C(0,﹣2),D(﹣3,﹣2).


(1)AB,CD 的位置關系為 ;△BCD 的面積為 ;S△ACD S△BCD(填兩者之間的數量關系);
(2)如圖 1,若∠1=100°,∠ACB=65°,求∠CAB 的度數;
(3)如圖 2,若∠ADC=∠DAC,∠ACB 的平分線 CE 交 DA 的延長線于點 E,在 B 點的運動過程中![]() 的值是否變化?若不變,直接寫出其值;若變化,請說明理由.(注:三角形內角和等于 180°)
的值是否變化?若不變,直接寫出其值;若變化,請說明理由.(注:三角形內角和等于 180°)
查看答案和解析>>
科目:初中數學 來源: 題型:
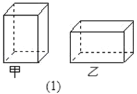
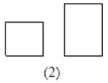
【題目】某紙品加工廠利用邊角料裁出正方形和長方形兩種硬紙片,長方形的寬與正方形的邊長相等(如圖2),再將它們制作成甲乙兩種無蓋的長方體小盒(如圖1).現將300張長方形硬紙片和150張正方形硬紙片全部用于制作這兩種小盒,可以做成甲乙兩種小盒各多少個?(注:圖1中向上的一面無蓋)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,點E、F分別是AD、AB的中點,EF交AC于點G,那么AG:GC的值為( )
A.1:2
B.1:3
C.1:4
D.2:3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一條直線過點(0,4),且與拋物線y= ![]() x2交于A,B兩點,其中點A的橫坐標是﹣2.
x2交于A,B兩點,其中點A的橫坐標是﹣2.
(1)求這條直線的函數關系式及點B的坐標.
(2)在x軸上是否存在點C,使得△ABC是直角三角形?若存在,求出點C的坐標,若不存在,請說明理由.
(3)過線段AB上一點P,作PM∥x軸,交拋物線于點M,點M在第一象限,點N(0,1),當點M的橫坐標為何值時,MN+3MP的長度最大?最大值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一天,媽媽下班后從公司開車回家,途中想起忘了帶第二天早上開早會的一個文件夾,于是打電話讓辦公室王阿姨馬上從公司送來,同時媽媽也往回開,遇到王阿姨后停下說了幾句話,接著繼續開車回家.設媽媽從公司出發后所用時間為t,媽媽與家的距離為s.下面能反映s與t的函數關系的大致圖象是( )
A.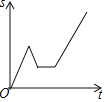 B.
B.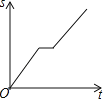
C. D.
D.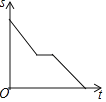
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△DAC和△EBC均是等邊三角形,AE、BD分別與CD、CE交于點M、N,且A、C、B在同一直線上,有如下結論:①△ACE≌△DCB;②CM=CN;③AC=DN;④PC平分∠APB;⑤∠APD=60°,其中正確結論有( )

A. 5個 B. 4個 C. 3個 D. 2個
查看答案和解析>>
科目:初中數學 來源: 題型:
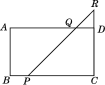
【題目】如圖,在長方形ABCD中,AB=4,BC=7,點P是BC邊上與點B不重合的動點,過點P的直線交CD的延長線于點R,交AD于點Q(點Q與點D不重合),且∠RPC=45°.設BP=x,梯形ABPQ的面積為y,求y與x之間的函數關系式,并求出自變量x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com