
【題目】已知△ABC 中,∠A=60°,∠ACB=40°,D為BC邊延長線上一點,BM平分∠ABC,E為射線BM上一點.
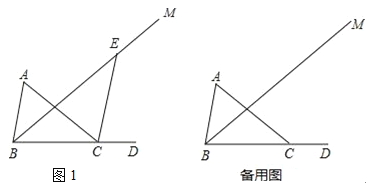
(1)如圖1,連接CE,
①若CE∥AB,求∠BEC的度數;
②若CE平分∠ACD,求∠BEC的度數.
(2)若直線CE垂直于△ABC的一邊,請直接寫出∠BEC的度數.
【答案】(1)①40°;②30°;(2)50°,130°,10°
【解析】試題分析:(1)①根據三角形的內角和得到∠ABC=80°,由角平分線的定義得到∠ABE=![]() ∠ABC=40°,根據平行線的性質即可得到結論;
∠ABC=40°,根據平行線的性質即可得到結論;
②根據鄰補角的定義得到∠ACD=180°-∠ACB=140°,根據角平分線的定義得到∠CBE=![]() ∠ABC=40°,∠ECD=
∠ABC=40°,∠ECD=![]() ∠ACD=70°,根據三角形的外角的性質即可得到結論;
∠ACD=70°,根據三角形的外角的性質即可得到結論;
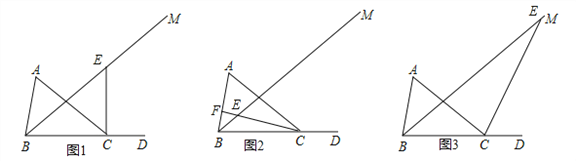
(2)①如圖1,當CE⊥BC時,②如圖2,當CE⊥AB于F時,③如圖3,當CE⊥AC時,根據垂直的定義和三角形的內角和即可得到結論.
試題解析:(1)①∵∠A=60°,∠ACB=40°,
∴∠ABC=80°,
∵BM平分∠ABC,
∴∠ABE=![]() ∠ABC=40°,
∠ABC=40°,
∵CE∥AB,
∴∠BEC=∠ABE=40°;
②∵∠A=60°,∠ACB=40°,
∴∠ABC=80°,∠ACD=180°-∠ACB=140°,
∵BM平分∠ABC,CE平分∠ACD,
∴∠CBE=![]() ∠ABC=40°,∠ECD=
∠ABC=40°,∠ECD=![]() ∠ACD=70°,
∠ACD=70°,
∴∠BEC=∠ECD-∠CBE=30°;
(2)①如圖1,當CE⊥BC時,
∵∠CBE=40°,
∴∠BEC=50°;
②如圖2,當CE⊥AB于F時,
∵∠ABE=40°,
∴∠BEC=90°+40°=130°,
③如圖3,當CE⊥AC時,
∵∠CBE=40°,∠ACB=40°,
∴∠BEC=180°-40°-40°-90°=10°.


 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案科目:初中數學 來源: 題型:
【題目】為了解某種電動汽車的性能,對這種電動汽車進行了抽檢,將一次充電后行駛的里程數分為A,B,C,D四個等級,其中相應等級的里程依次為200千米,210千米,220千米,230千米,獲得如下不完整的統計圖.

根據以上信息,解答下列問題:
(1)問這次被抽檢的電動汽車共有幾輛?并補全條形統計圖;
(2)估計這種電動汽車一次充電后行駛的平均里程數為多少千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有四包真空包裝的火腿腸,每包以標準質量450g為基準,超過的克數記作正數,不足的克數記作負數.下面的數據是記錄結果,其中與標準質量最接近的是( )
A. +2 B. ﹣3 C. +4 D. ﹣1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某游泳館普通票價20元/張,暑假為了促銷,新推出兩種優惠卡:
①金卡售價600元/張,每次憑卡不再收費.
②銀卡售價150元/張,每次憑卡另收10元.
暑假普通票正常出售,兩種優惠卡僅限暑假使用,不限次數.設游泳x次時,所需總費用為y元
(1)分別寫出選擇銀卡、普通票消費時,y與x之間的函數關系式;
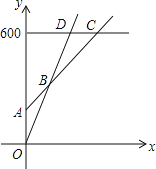
(2)在同一坐標系中,若三種消費方式對應的函數圖象如圖所示,請求出點A、B、C的坐標;
(3)請根據函數圖象,直接寫出選擇哪種消費方式更合算.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人玩摸球游戲,從放有足夠多球的箱子中摸球,規定每人最多兩種取法,甲每次摸4個或(3-k)個,乙每次摸5個或(5-k)個(k是常數,且0<k<3);經統計,甲共摸了16次,乙共摸了17次,并且乙至少摸了兩次5個球,最終兩人所摸出的球的總個數恰好相等,那么箱子中至少有球__________個.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com