
【題目】如圖,將矩形ABCD沿直線EF折疊,使點C與點A重合,折痕交AD于點E,交BC于點F,連接AF、CE,
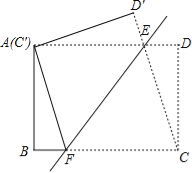
(1)求證:四邊形AFCE為菱形;
(2)設AE=a,ED=b,DC=c.請寫出一個a、b、c三者之間的數量關系式.
【答案】(1)證明見解析,(2)a2=b2+c2.
【解析】試題分析:(1)由矩形ABCD與折疊的性質,易證得△CEF是等腰三角形,即CE=CF,即可證得AF=CF=CE=AE,即可得四邊形AFCE為菱形;
(2)由折疊的性質,可得CE=AE=a,在Rt△DCE中,利用勾股定理即可求得:a、b、c三者之間的數量關系式為:a2=b2+c2.
試題解析:(1)證明:∵四邊形ABCD是矩形,
∴AD∥BC,
∴∠AEF=∠EFC,
由折疊的性質,可得:∠AEF=∠CEF,AE=CE,AF=CF,
∴∠EFC=∠CEF,
∴CF=CE,
∴AF=CF=CE=AE,
∴四邊形AFCE為菱形;
(2)a、b、c三者之間的數量關系式為:a2=b2+c2.
理由:由折疊的性質,得:CE=AE,
∵四邊形ABCD是矩形,
∴∠D=90°,
∵AE=a,ED=b,DC=c,
∴CE=AE=a,
在Rt△DCE中,CE2=CD2+DE2,
∴a、b、c三者之間的數量關系式為:a2=b2+c2.


 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:初中數學 來源: 題型:
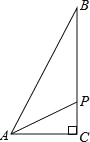
【題目】如圖,在Rt△ABC中,∠C=90°,AC=1cm,BC=2cm,點P從點A出發,以1cm/s的速度沿折線AC→CB→BA運動,最終回到點A,設點P的運動時間為x(s),線段AP的長度為y(cm),則能夠反映y與x之間函數關系的圖象大致是( )
A.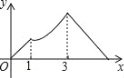 B.
B.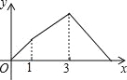 C.
C.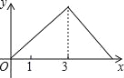 D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
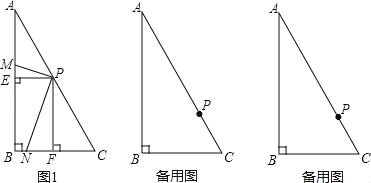
【題目】已知:在Rt△ABC,∠ABC=90°,∠C=60°,現將一個足夠大的直角三角板的頂點P放在斜邊AC上.
(1)設三角板的兩直角邊分別交邊AB、BC于點M、N.
①當點P是AC的中點時,分別作PE⊥AB于點E,PF⊥BC于點F,得到圖1,寫出圖中的一對全等三角形;
②在①的條件下,寫出與△PEM相似的三角形,并直接寫出PN與PM的數量關系.
(2)移動點P,使AP=2CP,將三角板繞點P旋轉,設旋轉過程中三角板的兩直角邊分別交邊AB、BC于點M、N(PM不與邊AB垂直,PN不與邊BC垂直);或者三角板的兩直角邊分別交邊AB、BC的延長線與點M、N.
③請在備用圖中畫出圖形,判斷PM與PN的數量關系,并選擇其中一種圖形證明你的結論;
④在③的條件下,當△PCN是等腰三角形時,若BC=3cm,則線段BN的長是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com