
【題目】如圖,第一角限內的點A在反比例函數 ![]() 的圖象上,第四象限內的點B 在反比例函數
的圖象上,第四象限內的點B 在反比例函數 ![]() 圖象上,且OA⊥OB,∠OAB=60度,則k值為 .
圖象上,且OA⊥OB,∠OAB=60度,則k值為 . 
【答案】-6
【解析】解:作AC⊥y軸于C,BD⊥y軸于D,如圖, 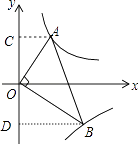
設A(a, ![]() ),B(b,
),B(b, ![]() ),
),
∵∠AOB=90°,
∴∠AOC+∠DOB=90°,
而∠AOC+∠OAC=90°,
∴∠OAC=∠DOB,
∴Rt△OAC∽Rt△BOD,
∴ ![]() ,
,
∵在Rt△AOB中,tan∠OAB=tan60°= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,
,
∴ab=2 ![]() ,
,
∴k=﹣ ![]() ab=﹣
ab=﹣ ![]() ×2
×2 ![]() =﹣6.
=﹣6.
所以答案是﹣6.
【考點精析】利用相似三角形的判定與性質對題目進行判斷即可得到答案,需要熟知相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方.


 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:初中數學 來源: 題型:
【題目】
![]()
(1)數軸上表示5與﹣2兩點之間的距離是 ,
(2)數軸上表示x與2的兩點之間的距離可以表示為 .
(3)如果|x﹣2|=5,則x= .
(4)同理|x+3|+|x﹣1|表示數軸上有理數x所對應的點到﹣3和1所對應的點的距離之和,請你找出所有符合條件的整數x,使得|x+3|+|x﹣1|=4,這樣的整數是 .
(5)由以上探索猜想對于任何有理數x,|x﹣3|+|x﹣6|是否有最小值?如果有,直接寫出最小值;如果沒有,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把一副三角板如圖(1)放置,其中∠ACB=∠DEC=90°,斜邊AB=6,DC=7,把三角板DCE繞著點C順時針旋轉使CD邊恰好過AB的中點O,得到△D1CE1如圖(2),則線段AD1的長度為( )

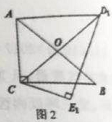
A. 3![]() B. 5 C. 4 D.
B. 5 C. 4 D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
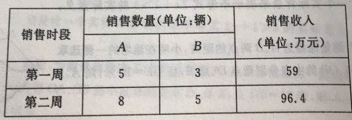
【題目】2017年12月29日鄭州市人民政府通告:為減少機動車污染物排放,持續改善我市空氣質量,從2018年1月1日起,每周工作日的7時至21時鄭州市東三環、南三環、西三環、北三環以內區域的所有道路限行按機動車號牌(含臨時號牌和外地號牌)最后一位阿拉伯數字(尾數為字母的以末尾數字為準),工作日每天限行2個號,即:號碼最后一位阿拉伯數字為1和6的機動車周一限行,2和7的機動車周二限行,3和8的機動車周三限4和9的機動車周四限行,5和0的機動車周五限行,因法定節假日放假、調休而調整為上班的周六、周日按對應調體的工作日限行但通告中還規定,懸掛新能源專用牌的新能源汽車不受限制.限行通告發布后,新能源汽車成為暢銷車型,某4S店銷售每輛進價分別為5萬元、9萬元的A、B兩種型號的新能源汽車,下表是近兩周的銷售情況:
(1)求A、B兩種型號的新能源汽車的銷售單價;(共
(2)若4S店準備用不超過200萬元的金額采購這兩種型號的新能源汽車共30輛,求B型號的新能源汽車最多能采購多少輛?
(進價、售價均保持不變,利潤=銷售收入一進貨成本)
(3在(2)的條件下,4S銷售完這230輛新能源汽車時45店的最大利潤是多少?并寫
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點C是半徑為1的半圓弧AB的一個三等分點,分別以弦AC、BC為直徑向外側作2個半圓,點D、E也分別是2半圓弧的三等分點,再分別以弦AD、DC、CE、BE為直徑向外側作4個半圓.則圖中陰影部分(4個新月牙形)的面積和是( )
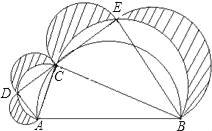
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是放在地面上的一個長方體盒子,其中AB=18cm,BC=12cm,BF=10cm,點M在棱AB上,且AM=6cm,點N是FG的中點,一只螞蟻要沿著長方體盒子的表面從點M爬行到點N,它需要爬行的最短路程為____.

查看答案和解析>>
科目:初中數學 來源: 題型:
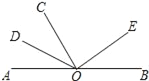
【題目】如圖,點O在直線AB上,OD是∠AOC的平分線,射線OE在∠BOC內.
(1)圖中有多少個小于180°的角?
(2)若OE平分∠BOC,求∠DOE的度數;
(3)若∠COE=2∠BOE,∠DOE=108°,求∠COE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據要求完成下列題目:
(1)如圖中有________塊小正方體;
(2) 請在下面方格紙中分別畫出它的左視圖和俯視圖(畫出的圖都用鉛筆涂上陰影);
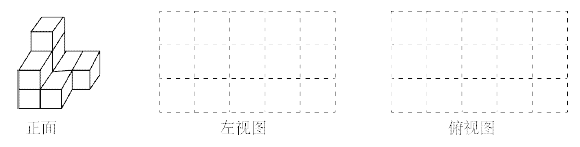
(3)用小正方體搭一個幾何體,使得它的俯視圖和左視圖與你在上圖方格中所畫的圖一致,則這樣的幾何體最少要________個小正方體,最多要________個小正方體.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com