
【題目】閱讀理解:
我們知道:一條線段有兩個端點,線段![]() 和線段
和線段![]() 表示同一條線段. 若在直線
表示同一條線段. 若在直線![]() 上取了三個不同的點,則以它們為端點的線段共有 條;若取了四個不同的點,則共有線段 條;…;依此類推,取了
上取了三個不同的點,則以它們為端點的線段共有 條;若取了四個不同的點,則共有線段 條;…;依此類推,取了![]() 個不同的點,共有線段條.(用含
個不同的點,共有線段條.(用含![]() 的代數式表示)
的代數式表示)
類比探究:
以一個銳角的頂點為端點向這個角的內部引射線.
(1)若引出兩條射線,則所得圖形中共有 個銳角;
(2)若引出![]() 條射線,則所得圖形中共有 個銳角.(用含
條射線,則所得圖形中共有 個銳角.(用含![]() 的代數式表示)
的代數式表示)
拓展應用:
一條鐵路上共有8個火車站,若一列火車往返過程中必須停靠每個車站,則鐵路局需為這條線路準備多少種車票?
【答案】![]() ; (1)6; (2)
; (1)6; (2) ![]() ; 拓展應用: 鐵路局需為這條線路準備56種車票.
; 拓展應用: 鐵路局需為這條線路準備56種車票.
【解析】
對于“閱讀理解”,假如l上取三點A,B,C,則線段有AB,AC,BC,自己試著總結出規律,再根據線段的定義解答;
類比探究:根據角的定義解答;
拓展應用:先計算出線段的條數,再根據兩站之間需要兩種車票解答.
解答:
閱讀理三個不同的點,以它們為端點的線段共有3條,
若取了四個不同的點,則共有線段6條,…,
依此類推,取了n個不同的點,共有線段n(n1)2條;
類比探究:

(1)引出兩條射線,共有4條射線,銳角的個數為6;
(2)引出n條射線,共有n+2條射線,銳角的個數:![]() ;
;
拓展應用:8個火車站共有線段條數![]() =28,
=28,
需要車票的種數:28×2=56.
故答案為:3,6,![]() ;6;
;6;![]() ;56.
;56.


科目:初中數學 來源: 題型:
【題目】有一個面積為1的正方形,經過一次“生長”后,在它的左右肩上生出兩個小正方形(如圖1),其中,三個正方形圍成的三角形是直角三角形,再經過一次“生長”后,生出了4個正方形(如圖2),如果按此規律繼續“生長”下去,它將變得“枝繁葉茂”.在“生長”了2 017次后形成的圖形中所有正方形的面積和是____ .


圖1 圖2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個自然數的立方,可以分裂成若干個連續奇數的和,例如:23,33和43分別可以按如圖所示的方式“分裂”,則63“分裂”出的奇數中,最大的奇數是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,頂點為A( ![]() ,1)的拋物線經過坐標原點O,與x軸交于點B.
,1)的拋物線經過坐標原點O,與x軸交于點B.
(1)求拋物線對應的二次函數的表達式;
(2)過B作OA的平行線交y軸于點C,交拋物線于點D,求證:△OCD≌△OAB;
(3)在x軸上找一點P,使得△PCD的周長最小,求出P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線CD與EF相交于點O,∠COE=60°,將一直角三角尺AOB的直角頂點與O重合,OA平分∠COE.
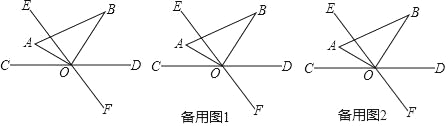
(1)求∠BOD的度數;
(2)將三角尺AOB以每秒3°的速度繞點O順時針旋轉,同時直線EF也以每秒9°的速度繞點O順時針旋轉,設運動時間為t秒(0≤t≤40).
①當t為何值時,直線EF平分∠AOB;
②若直線EF平分∠BOD,直接寫出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小明想測山高度,他在B處仰望山頂A,測得仰角∠B=31°,再往山的方向(水平方向)前進80m至索道口C處,沿索道方向仰望山頂,測得仰角∠ACE=39°.求這座山的高度(小明的身高忽略不計).
【參考數據:tan31°≈ ![]() ,sin31°≈
,sin31°≈ ![]() ,tan39°≈
,tan39°≈ ![]() ,sin39°≈
,sin39°≈ ![]() 】
】
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:有一組對角相等而另一組對角不相等的凸四邊形叫做“等對角四邊形”.
(1)已知:如圖1,四邊形ABCD是“等對角四邊形”,∠A≠∠C,∠A=70°,∠B=80°.求∠C,∠D的度數.
(2)在探究“等對角四邊形”性質時:張同學畫了一個“等對角四邊形”ABCD(如圖2),其中∠ABC=∠ADC,AB=AD,此時她發現CB=CD成立.請你證明此結論;
(3)已知:在“等對角四邊形”ABCD中,∠DAB=45°,∠ABC=90°,AB=5,AD=4 ![]() .則對角線AC的長為 .
.則對角線AC的長為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程解應用題:五蓮縣新瑪特購物中心第一次用5000元購進甲、乙兩種商品,其中乙商品的件數比甲商品件數的![]() 倍多15件,甲、乙兩種商品的進價和售價如下表(注:獲利=售價﹣進價)
倍多15件,甲、乙兩種商品的進價和售價如下表(注:獲利=售價﹣進價)
甲 | 乙 | |
進價(元/件) | 20 | 30 |
售價(元/件) | 29 | 40 |
(1)新瑪特購物中心將第一次購進的甲、乙兩種商品全部賣完后一共可獲得多少利潤?
(2)該購物中心第二次以第一次的進價又購進甲、乙兩種商品,其中甲種商品的件數不變,乙種商品的件數是第一次的3倍;甲商品按原價銷售,乙商品打折銷售,第二次兩種商品都銷售完以后獲得總利潤比第一次獲得的總利潤多160元,求第二次乙種商品是按原價打幾折銷售?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(![]() )如圖①,在四邊形
)如圖①,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 上的點,且
上的點,且![]() .
.
求證:![]() .
.
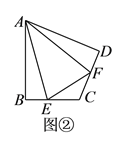
(![]() )如圖②,在四邊形
)如圖②,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 上的點,且
上的點,且![]() ,(
,(![]() )中的結論是否仍然成立?
)中的結論是否仍然成立?
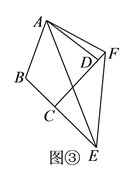
(![]() )如圖③,在四邊形
)如圖③,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 延長線上的點,且
延長線上的點,且![]() .(
.(![]() )中的結論是否仍然成立?若成立,請證明;若不成立,請寫出它們之間的數量關系,并證明.
)中的結論是否仍然成立?若成立,請證明;若不成立,請寫出它們之間的數量關系,并證明.
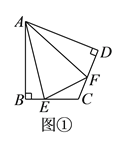
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com