
【題目】在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列條件中不能判定這兩個三角形相似的是( )
A. ∠A=55°,∠D=35°
B. AC=9,BC=12,DF=6,EF=8
C. AC=3,BC=4,DF=6,DE=8
D. AB=10,AC=8,DE=15,EF=9
科目:初中數學 來源: 題型:
【題目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.則下列結論: ①∠BOE=![]() (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正確結論__________(填編號).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正確結論__________(填編號).

查看答案和解析>>
科目:初中數學 來源: 題型:
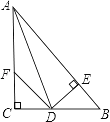
【題目】如圖:在△ABC中,∠C=90°,AD是∠BAC的平分線,DE⊥AB于E,F在AC上,BD=DF;
求證:(1)CF=EB.
(2)AB=AF+2EB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了加強校園周邊治安綜合治理,警察巡邏車在學校旁邊的一條東西方向的公路上執行治安巡邏,如果規定向東為正,向西為負,從出發點開始所走的路程(單位:千米)為:![]()
(1)此時,這輛巡邏車司機如何向警務處描述他現在的位置?
(2)已知每千米耗油![]() 升,如果警務處命令其巡邏車馬上返回出發點,這次巡邏共耗油多少升?
升,如果警務處命令其巡邏車馬上返回出發點,這次巡邏共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
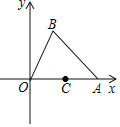
【題目】在平面直角坐標系中,點A、B、C的坐標分別為![]() ,
,![]() ,
,![]() ,點P,Q是
,點P,Q是![]() 邊上的兩個動點
邊上的兩個動點![]() 點P不與點C重合
點P不與點C重合![]() ,以P,O,Q為頂點的三角形與
,以P,O,Q為頂點的三角形與![]() 全等,則滿足條件的點P的坐標為______.
全等,則滿足條件的點P的坐標為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=BC=6cm,點P從點A出發,沿AB方向以每秒![]() cm的速度向終點B運動;同時,動點Q從點B出發沿BC方向以每秒1cm的速度向終點C運動,將△PQC沿BC翻折,點P的對應點為點P′.設點Q運動的時間為t秒,若四邊形QPCP′為菱形,則t的值為( )
cm的速度向終點B運動;同時,動點Q從點B出發沿BC方向以每秒1cm的速度向終點C運動,將△PQC沿BC翻折,點P的對應點為點P′.設點Q運動的時間為t秒,若四邊形QPCP′為菱形,則t的值為( )
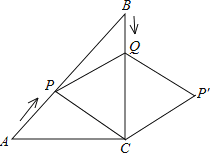
A. ![]() B. 2 C. 2
B. 2 C. 2![]() D. 3
D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
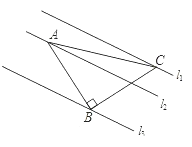
【題目】如圖,已知△ABC中,∠ABC=90°,AB=BC,三角形的頂點在相互平行的三條直線l1,l2,l3上,且l1、l2之間的距離為2,l2、l3之間的距離為3,則AC的長是_________;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,E為BC上一點,以CE為直徑作⊙O,AB與⊙O相切于點D,連接CD,若BE=OE=2.
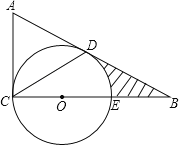
(1)求證:∠A=2∠DCB;
(2)求圖中陰影部分的面積(結果保留π和根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,回答提出的問題.
我們知道:一個數![]() 的絕對值可以表示成
的絕對值可以表示成![]() ,它是一個非負數,在數軸上,
,它是一個非負數,在數軸上,![]() 表示
表示![]() 這個數在數軸上所對應的點到原點的距離(距離,當然不可能是負數),這正是絕對值的幾何意義,比如說
這個數在數軸上所對應的點到原點的距離(距離,當然不可能是負數),這正是絕對值的幾何意義,比如說![]() 表示2這個數在數軸上所對應的點到原點的距離,它是2,所以說
表示2這個數在數軸上所對應的點到原點的距離,它是2,所以說![]() 表示
表示![]() 這個數在數軸上所對應的點到原點的距離,它也是2,所以說
這個數在數軸上所對應的點到原點的距離,它也是2,所以說![]() ,嚴格來說,在數軸上,一個數
,嚴格來說,在數軸上,一個數![]() 在數軸上所對應的點到原點(原點對應的數為0)的距離應該表示為
在數軸上所對應的點到原點(原點對應的數為0)的距離應該表示為![]() ,但平時我們都寫成
,但平時我們都寫成![]() ,原因你明白.
,原因你明白.
(1)若給定![]() ,要找這樣的x,請按照上面材料中的說法,解釋它的幾何意義并找出對應的
,要找這樣的x,請按照上面材料中的說法,解釋它的幾何意義并找出對應的![]() ;
;
(2)實際上,對于數軸上任意兩個數![]() 之間的距離我們也可以表示為
之間的距離我們也可以表示為![]() ,反過來,
,反過來,![]() 這個絕對值的幾何意義就是:數軸上表示
這個絕對值的幾何意義就是:數軸上表示![]() 與
與![]() 這兩個數的點之間的距離,你能結合上面的敘述,解釋
這兩個數的點之間的距離,你能結合上面的敘述,解釋![]() 的幾何意義嗎?請按你的理解說明:
的幾何意義嗎?請按你的理解說明:![]() 呢,如果能解釋這個,你了不起;
呢,如果能解釋這個,你了不起;
(3)若![]() ,請直接寫出
,請直接寫出![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com