
【題目】如圖,在平行四邊形![]() 中,以點
中,以點![]() 為圓心,
為圓心, ![]() 為半徑的圓,交
為半徑的圓,交![]() 于點
于點![]() .
.
(1)求證: ![]() ≌
≌![]() ;
;
(2)如果![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的長.
的長.

【答案】(1)證明見解析;(2)EC=![]() .
.
【解析】試題分析:(1)根據(jù)平行四邊形的性質(zhì)得出AD=BC,根據(jù)圓的半徑相等可得出AB=AE,結(jié)合等腰三角形的性質(zhì)和平行線的性質(zhì)可得出∠B=∠EAD,從而利用SAS可證得結(jié)論;(2)在RT△ABC中,可求出BC,過圓心A作AH⊥BC,垂足為H,則BH=HE,則結(jié)合cos∠B的值,可求出BH、EH的長度,繼而根據(jù)EC=BC-BE即可得出答案.
試題解析:(1)∵四邊形ABCD是平行四邊形,
∴AD=BC,AD∥BC,
∴∠AEB=∠EAD,
∵AB=AE(AB與AE為圓的半徑),
∴∠AEB=∠B,
∴∠B=∠EAD,
在△ABC和△EAD中,  ,
,
故可得△ABC≌△EAD.
(2)∵AB⊥AC,
∴∠BAC=90°,
在Rt△ABC中,cos∠B=![]() ,
,
又∵cos∠B=![]() ,AB=6,
,AB=6,
∴BC=10,
過圓心A作AH⊥BC,垂足為H,
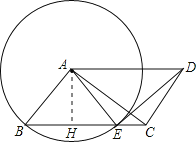
則BH=HE,
在Rt△ABH中,cos∠B=![]() ,
,
則可得![]() ,
,
解得:BH=![]() ,
,
∴BE=![]() ,
,
故可得EC=BCBE=![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,O為坐標(biāo)原點,點A的坐標(biāo)為(-8,0),直線BC經(jīng)過點B(-8,6),C(0,6),將四邊形OABC繞點O按順時針方向旋轉(zhuǎn)α度(0<α ≤180°)得到四邊形OA′B′C′,此時直線OA′、直線B′C′分別與直線BC相交于P、Q.在四邊形OABC旋轉(zhuǎn)過程中,若BP=![]() BQ,則點P的坐標(biāo)為__________.
BQ,則點P的坐標(biāo)為__________.
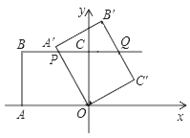
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在平面直角坐標(biāo)系中,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() 、
、![]() ,點
,點![]() 為
為![]() 軸負(fù)半軸上一點,
軸負(fù)半軸上一點, ![]() 于點
于點![]() 交
交![]() 軸于點
軸于點![]() .已知拋物線
.已知拋物線![]() 經(jīng)過點
經(jīng)過點![]() 、
、![]() 、
、![]() .
.
(![]() )求拋物線的函數(shù)式.
)求拋物線的函數(shù)式.
(![]() )連接
)連接![]() ,點
,點![]() 在線段
在線段![]() 上方的拋物線上,連接
上方的拋物線上,連接![]() 、
、![]() ,若
,若![]() 和
和![]() 面積滿足
面積滿足![]() ,求點
,求點![]() 的坐標(biāo).
的坐標(biāo).
(![]() )如圖
)如圖![]() ,
, ![]() 為
為![]() 中點,設(shè)
中點,設(shè)![]() 為線段
為線段![]() 上一點(不含端點),連接
上一點(不含端點),連接![]() .一動點
.一動點![]() 從
從![]() 出發(fā),沿線段
出發(fā),沿線段![]() 以每秒
以每秒![]() 個單位的速度運(yùn)動到
個單位的速度運(yùn)動到![]() ,再沿著線段
,再沿著線段![]() 以每秒
以每秒![]() 個單位的速度運(yùn)動到
個單位的速度運(yùn)動到![]() 后停止.若點
后停止.若點![]() 在整個運(yùn)動過程中用時最少,請直接寫出最少時間和此時點
在整個運(yùn)動過程中用時最少,請直接寫出最少時間和此時點![]() 的坐標(biāo).
的坐標(biāo).
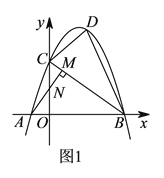
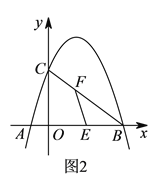
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,Rt△ABC中,∠ACB=90。 , 直角邊AC在射線OP上,直角頂點C與射線端點0重合,AC=b,BC=a,且滿足 ![]() .
.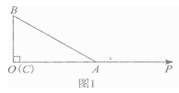
(1)求a,b的值;
(2)如圖2,向右勻速移動Rt△ABC,在移動的過程中Rt△ABC的直角邊AC在射線OP上勻速向右運(yùn)動,移動的速度為1個單位/秒,移動的時間為t秒,連接OB,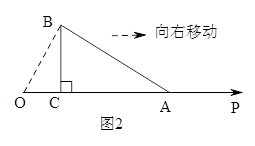
①若△OAB為等腰三角形,求t的值;
②Rt△ABC在移動的過程中,能否使△OAB為直角三角形?若能,求出t的值:若不能,說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com