
【題目】如圖,已知在ABCD中,E,F是對角線BD上的兩點,則以下條件不能判斷四邊形AECF為平行四邊形的是( ) 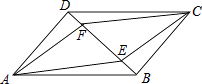
A.BE=DF
B.AF⊥BD,CE⊥BD
C.∠BAE=∠DCF
D.AF=CE
【答案】D
【解析】解:如圖,連接AC與BD相交于O, 在ABCD中,OA=OC,OB=OD,
要使四邊形AECF為平行四邊形,只需證明得到OE=OF即可;
A、若BE=DF,則OB﹣BE=OD﹣DF,即OE=OF,故本選項錯誤;
B、若AF⊥BD,CE⊥BD,則可以利用“角角邊”證明△ADF和△CBE全等,從而得到DF=BE,然后同A,故本選項錯誤;
C、∠BAE=∠DCF能夠利用“角角邊”證明△ABE和△CDF全等,從而得到DF=BE,然后同A,故本選項錯誤;
D、AF=CE無法證明得到OE=OF,故本選項正確.
故選D.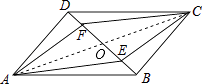
【考點精析】根據題目的已知條件,利用平行四邊形的判定與性質的相關知識可以得到問題的答案,需要掌握若一直線過平行四邊形兩對角線的交點,則這條直線被一組對邊截下的線段以對角線的交點為中點,并且這兩條直線二等分此平行四邊形的面積.


科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c中x和y的值如下表:( )
x | 0.10 | 0.11 | 0.12 | 0.13 | 0.14 |
y | -5.6 | -3.1 | -1.5 | 0.9 | 1.8 |
則ax2+bx+c=0的一個根的范圍是( )
A.0.10<x<0.11B.0.11<x<0.12C.0.12<x<0.13D.0.13<x<0.14
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,點D為斜邊AB的中點,BC=6,CD=5,過點A作AE⊥AD且AE=AD,過點E作EF垂直于AC邊所在的直線,垂足為點F,連接DF,請你畫出圖形,并直接寫出線段DF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D為AB邊上一點.
(1)求證:△ACE≌△BCD;
(2)求證:![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
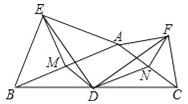
【題目】如圖,在鈍角△ABC中,點D是BC的中點,分別以AB和AC為斜邊向△ABC的外側作等腰直角三角形ABE和等腰直角三角形ACF,M、N分別為AB、AC的中點,連接DM、DN、DE、DF、EM、EF、FN.求證:
(1)△EMD≌△DNF;
(2)△EMD∽△EAF;
(3)DE⊥DF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知O為直線AD上一點,射線OC,射線OB,∠AOC與∠AOB互補,OM,ON分別為∠AOC,∠AOB的平分線,若∠MON=40°.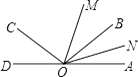
(1)∠COD與∠AOB相等嗎?請說明理由;
(2)試求∠AOC與∠AOB的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com