【題目】如圖,在平面直角坐標系中,A(-1，5)，B（-1，0），C（-4，3）.
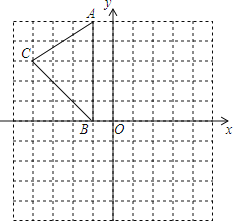
（1）在圖中作出△ABC關于y軸的對稱圖形△A1B1C1；
（2）寫出點A1、B1、C1的坐標；
（3）在y軸上畫出點P，使PA+PC最小；
（4）求六邊形AA1C1B1BC的面積．.
【答案】（1）作圖見解析；（2）A1（1，5）、B1（1，0）、C1（4，3）；（3）見解析；（4）25.
【解析】試題分析：（1）根據題意畫出△A1B1C1即可；
（2）根據△A1B1C1在坐標系中的位置即可得出各點坐標；
（3）連接A1C與y軸交于點P，則P點即為所求；
（4）根據S六邊形AA1C1B1BC=S△ABC+S△A1B1C1+S矩形AA1C1B1B即可得出結論．
試題解析：（1）如圖所示；
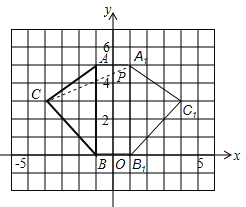
（2）由圖可知，A1（1，5）、B1（1，0）、C1（4，3）；
（3）連接A1C與y軸交于點P，則P點即為所求；
（4）S六邊形AA1C1B1BC=S△ABC+S△A1B1C1+S矩形AA1C1B1B
=
×5×3+
×5×3+2×5
=15+10
=25．
云南師大附小一線名師提優作業系列答案
沖刺100分單元優化練考卷系列答案科目：初中數學 來源： 題型：
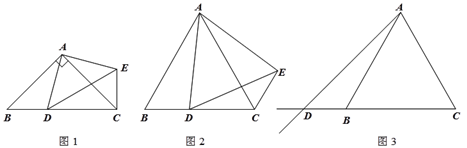
【題目】在△ABC中，AB=AC，點D是射線CB上的一動點（不與點B、C重合），以AD為一邊在AD的右側作△ADE，使AD=AE，∠DAE=∠BAC，連接CE．
（1）如圖1，當點D在線段CB上，且∠BAC=90°時，那么∠DCE= 度；
（2）設∠BAC= 
，∠DCE= 
．
① 如圖2，當點D在線段CB上，∠BAC≠90°時，請你探究
與
之間的數量關系，并證明你的結論；
② 如圖3，當點D在線段CB的延長線上，∠BAC≠90°時，請將圖3補充完整，并直接寫出此時
與
之間的數量關系（不需證明）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，△DEF是由△ABC繞點O順時針旋轉180°后形成的圖形；
(1)請你指出圖中所有相等的線段；
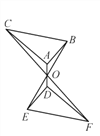
(2)圖中哪些三角形可以被看成是關于點O成中心對稱關系？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】拋物線
與
軸交于點A，點B（1，0），與
軸交于點C（0，﹣3），點M是其頂點．
（1）求拋物線解析式；
（2）第一象限拋物線上有一點D,滿足∠DAB=45°,求點D的坐標；
（3）直線
(﹣3＜
＜﹣1)與x軸相交于點H．與線段AC，AM和拋物線分別相交于點E，F，P．證明線段HE，EF，FP總能組成等腰三角形.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某蔬菜生產基地在氣溫較低時，用裝有恒溫系統的大棚栽培一種在自然光明且溫度為18
的條件下生長最快的新品種．如圖，是某天恒溫系統從開啟到關閉及關閉后，大棚內溫度y(
)隨時間x(小時)變化的函數圖象，其中BC段足雙曲線
的一部分，請根據圖中信息解答下列問題：
(1)恒溫系統這天保持大棚內溫度18
的時間有多少小時？
(2)求k值；
(3)當x=15時，大棚內的溫度約為多少度？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在直角坐標平面內，二次函數圖象的頂點為A（1，﹣4），且過點B（3，0）．
（1）求該二次函數的解析式；
（2）將該二次函數圖象向右平移幾個單位，可使平移后所得圖象經過坐標原點？并直接寫出平移后所得圖象與x軸的另一個交點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】問題探究
（
）如圖①，已知正方形
的邊長為
，點
和
分別是邊
、
上兩點，且
．連接
和
，交于點
．猜想
與
的位置關系，并證明你的結論．
（
）如圖②，已知正方形
的邊長為
，點
和
分別從點
、
同時出發，以相同的速度沿
、
方向向終點
和
運動，連接
和
，交于點
，求
周長的最大值．
問題解決
（
）如圖③，
為邊長為
的菱形
的對角線， 
．點
和
分別從點
、
同時出發；以相同的速度沿
、
向終點
和
運動，連接
和
，交于點
，求
周長的最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠A=60°，BD、CD分別平分∠ABC、∠ACB，M、N、Q分別在DB、DC、BC的延長線上，BE、CE分別平分∠MBC、∠BCN，BF、CF分別平分∠EBC、∠ECQ，則∠F=（ ）．
A. 60° B. 45° C. 30° D. 15°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
