
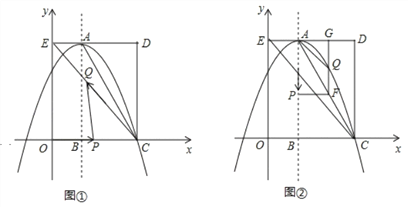
【題目】如圖,在平面直角坐標系中,矩形OCDE的三個頂點分別是C(3,0),D(3,4),E(0,4).點A在DE上,以A為頂點的拋物線過點C,且對稱軸x=1交x軸于點B.連接EC,AC.點P,Q為動點,設運動時間為t秒.
(1)填空:點A坐標為 ;拋物線的解析式為 .
(2)在圖1中,若點P在線段OC上從點O向點C以1個單位/秒的速度運動,同時,點Q在線段CE上從點C向點E以2個單位/秒的速度運動,當一個點到達終點時,另一個點隨之停止運動.當t為何值時,△PCQ為直角三角形?
(3)在圖2中,若點P在對稱軸上從點A開始向點B以1個單位/秒的速度運動,過點P做PF⊥AB,交AC于點F,過點F作FG⊥AD于點G,交拋物線于點Q,連接AQ,CQ.當t為何值時,△ACQ的面積最大?最大值是多少?
【答案】(1)點A坐標為(1,4),y=﹣x2+2x+3;(2)當t=![]() 或t=
或t=![]() 時,△PCQ為直角三角形;(3)當t=2時,△ACQ的面積最大,最大值是1.
時,△PCQ為直角三角形;(3)當t=2時,△ACQ的面積最大,最大值是1.
【解析】試題分析:(1)根據矩形的三個頂點坐標以及拋物線的對稱軸可求出點A的坐標;設拋物線的解析式為頂點式,然后把點A、C坐標代入計算即可;(2)分∠QPC=90°和∠PQC=90°兩種情況討論,利用比例線段可求出t的值;(3)求出直線AC的解析式,然后把點P(1,4﹣t)的縱坐標代入,然后用t可表示出點Q的坐標,以及QF的長,然后可求出△ACQ的面積與t的函數關系式,利用二次函數的性質確定函數值的值即可.
試題解析:解:(1)∵拋物線的對稱軸為x=1,矩形OCDE的三個頂點分別是C(3,0),D(3,4),E(0,4),點A在DE上,
∴點A坐標為(1,4),
設拋物線的解析式為y=a(x﹣1)2+4,
把C(3,0)代入拋物線的解析式,可得a(3﹣1)2+4=0,
解得a=﹣1.
故拋物線的解析式為y=﹣(x﹣1)2+4,即y=﹣x2+2x+3;
(2)依題意有:OC=3,OE=4,
∴CE=![]() =
=![]() =5,
=5,
當∠QPC=90°時,
∵cos∠QPC=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() ;
;
當∠PQC=90°時,
∵cos∠QCP=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() .
.
∴當t=![]() 或t=
或t=![]() 時,△PCQ為直角三角形;
時,△PCQ為直角三角形;
(3)∵A(1,4),C(3,0),
設直線AC的解析式為y=kx+b,則
![]() ,
,
解得![]() .
.
故直線AC的解析式為y=﹣2x+6.
∵P(1,4﹣t),將y=4﹣t代入y=﹣2x+6中,得x=1+![]() ,
,
∴Q點的橫坐標為1+![]() ,
,
將x=1+![]() 代入y=﹣(x﹣1)2+4中,得y=4﹣
代入y=﹣(x﹣1)2+4中,得y=4﹣![]() .
.
∴Q點的縱坐標為4﹣![]() ,
,
∴QF=(4﹣![]() )﹣(4﹣t)=t﹣
)﹣(4﹣t)=t﹣![]() ,
,
∴S△ACQ=S△AFQ+S△CPQ
=![]() FQAG+
FQAG+![]() FQDG
FQDG
=![]() FQ(AG+DG)
FQ(AG+DG)
=![]() FQAD
FQAD
=![]() ×2(t﹣
×2(t﹣![]() )
)
=﹣![]() (t﹣2)2+1,
(t﹣2)2+1,
∴當t=2時,△ACQ的面積最大,最大值是1.


科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=x+m的圖象與反比例函數y=![]() 的圖象交于A,B兩點,且與x軸交于點C,點A的坐標為(2,1).
的圖象交于A,B兩點,且與x軸交于點C,點A的坐標為(2,1).

(1)求m及k的值;
(2)求點C的坐標,并結合圖象寫出不等式組0<x+m≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)16﹣23+24﹣17
(2)﹣23÷(﹣ ![]() )÷(﹣
)÷(﹣ ![]() )2
)2
(3)( ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )×(﹣18)
)×(﹣18)
(4)(﹣1)10﹣(﹣3)×| ![]() ﹣
﹣ ![]() |÷
|÷ ![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,點E,F分別在BC,CD上, ΔAEF是等邊三角形,連接AC交EF于點G,下列結論:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE,其中結論正確的個數為( )
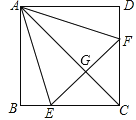
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:a是﹣1,且a、b、c滿足(c﹣6)2+|2a+b|=0,請回答問題:
(1)請直接寫出b、c的值:b= , c=
(2)在數軸上,a、b、c所對應的點分別為A、B、C,點P為易動點,其對應的數為x,
(a)當點P在AB間運動(不包括A、B),試求出P點與A、B、C三點的距離之和.
(b)當點P從A點出發,向右運動,請根據運動的不同情況,化簡式子:|x+1|﹣|x﹣2|+2|x﹣6|(請寫出化簡過程)![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如右圖,C為線段AE上一動點(不與點A,E重合),在AE同側分別作正三角形ABC和正三角形CDE、AD與BE交于點O,AD與BC交于點P,BE與CD交于點Q,連結PQ.以下五個結論:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°. 恒成立的結論有( )
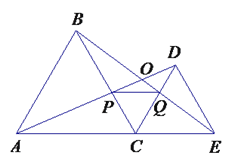
A. ①③④⑤ B. ①②④⑤
C. ①②③⑤ D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】電腦病毒傳播快,如果一臺電腦被感染,經過兩輪感染后就會有81臺電腦被感染,若每輪感染中平均一臺電腦會感染x臺電腦,下列方程正確的是( )
A.x(x+1)=81
B.1+x+x2=81
C.1+x+x(x+1)=81
D.1+(x+1)2=81
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com