Question

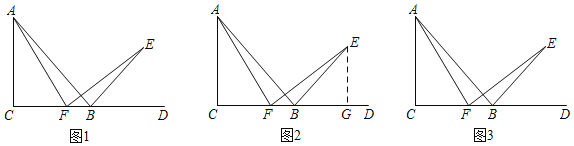
【題目】閱讀下面的操作過程,回答后面的問題:在一次數學實踐探究活動中,小強過A,C兩點畫直線AC把平行四邊形ABCD分割成兩個部分(如圖1),小剛過AB,CD的中點畫直線EF,把平行四邊形ABCD也分割成兩個部分(如圖2).

(1)這兩種分割方法中面積之間的關系為:S1　　S2,S3　　S4;

(2)根據這兩位同學的分割方法,你認為把平行四邊形分割成滿足以上面積關系的直線有　　條,請在圖3的平行四邊形中畫出一種;

(3)由上述實驗操作過程,你發現了什么規律?

Answer 1

【答案】（1）=，=（2）無數（3）見解析

【解析】

（1）都是相等關系，因為AC，EF都經過平行四邊形的對稱中心，故分得的兩部分的面積相等；（2）有無數條，因為經過對稱中心的直線即可,這樣的直線有無數條；（3）經過平行四邊形對稱中心的直線把平行四邊形的面積分成相等的兩份．

(1)這兩種分割方法中面積之間的關系為:S1　=　S2,S3　=　S4;

(2)根據這兩位同學的分割方法,你認為把平行四邊形分割成滿足以上面積關系的直線有　無數　條,請在圖3的平行四邊形中畫出一種;

(3)規律:經過平行四邊形兩條對角線交點的任意一條直線都把平行四邊形分成面積相等的兩部分.