【題目】在正方形ABCD中，CE=DF，求證：AE⊥BF．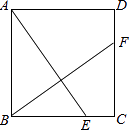 
【答案】證明：∵四邊形ABCD是正方形， 
∴∠ABE=∠C=90°，AB=BC，BC=CD，
∴CE=DF，
∴BE=CF，
在△ABE和△BCF中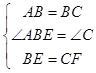
∴△ABE≌△BCF（SAS），
∴∠BAE=∠CBF，
∵∠ABE=90°，
∴∠BAE+∠AEB=90°，
∴∠CBF+∠AEB=90°，
∴∠BOE=180°﹣90°=90°，
∴AE⊥BF．
【解析】根據正方形性質得出∠ABE=∠C=90°，AB=BC，BC=CD，求出BE=CF，根據SAS推出△ABE≌△BCF，根據全等三角形的性質得出∠BAE=∠CBF，求出∠CBF+∠AEB=90°，即可得出答案．
【考點精析】根據題目的已知條件，利用正方形的性質的相關知識可以得到問題的答案，需要掌握正方形四個角都是直角，四條邊都相等；正方形的兩條對角線相等，并且互相垂直平分，每條對角線平分一組對角；正方形的一條對角線把正方形分成兩個全等的等腰直角三角形；正方形的對角線與邊的夾角是45o；正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形．
科目：初中數學 來源： 題型：
【題目】如圖，ABCD的對角線AC，BD相交于點O，點E，F分別是線段AO，BO的中點，若AC+BD=24厘米，△OAB的周長是18厘米，則EF=厘米．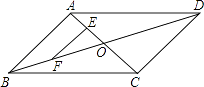 
查看答案和解析>>
科目：初中數學 來源： 題型：
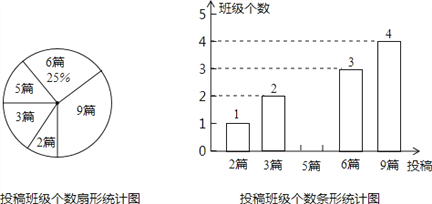
【題目】為積極響應市政府提出的“建設美麗南寧”的號召，我市某校在八，九年級開展征文活動，校學生會對這兩個年級各班內的投稿情況進行統計，并制成了如圖所示的兩幅不完整的統計圖．
（1）求扇形統計圖中投稿篇數為2所對應的扇形的圓心角的度數：
（2）求該校八，九年級各班在這一周內投稿的平均篇數，并將該條形統計圖補充完整．
（3）在投稿篇數為9篇的四個班級中，八，九年級各有兩個班，校學生會準備從這四個班中選出兩個班參加全市的表彰會，請你用列表法或畫樹狀圖的方法求出所選兩個班正好不在同一年級的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】實踐探究題
（1）
是不為1的有理數，我們把
稱為
的差倒數．如：2的差倒數是
， 
的差倒數是
．已知
， 
是
的差倒數， 
是
的差倒數， 
是
的差倒數，…，依此類推， 
的差倒數
________．
（2）觀察下列有規律的數： 
， 
， 
， 
， 
， 
…根據規律可知：
①第10個數是________， 
是第________個數．
②計算
________．（直接寫出答案即可）
（3）高斯函數[x]，也稱為取整函數，即[x]表示不超過x的最大整數．
例如：[2.3]＝2，[－1.5]＝－2.
則下列結論：①[－2.1]＋[1]＝－2；②[x]＋[－x]＝0；③[2.5]＋[－2.5]＝－1； ④[x＋1]＋[－x＋1]的值為2.
其中正確的結論有________ (填序號)．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
