【題目】如圖，矩形ABCD中，AB=4，BC=2，O為對角線AC的中點，點P、Q分別從A和B兩點同時出發，在邊AB和BC上勻速運動，并且同時到達終點B、C，連接PO、QO并延長分別與CD、DA交于點M、N．在整個運動過程中，圖中陰影部分面積的大小變化情況是（ ）
A. 一直增大 B. 一直減小 C. 先減小后增大 D. 先增大后減小
【答案】C
【解析】連接OB，根據點O是為對角線AC的中點可得△ABO和△BOC的面積相等，又點P、Q分別從A和B兩點同時出發，在邊AB和BC上勻速運動，并且同時到達終點B、C，連接PO、QO并延長分別與CD、DA交于點M、N．在整個運動過程中，然后把開始時、結束時、與中點時的△OPQ的面積與△ABC的面積相比即可進行判斷．
解：如圖所示，
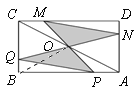
連接OB，∵O是AC的中點，
∴S△ABO=S△BOC=
S△ABC，
開始時，S△OBP=S△AOB=
S△ABC，
點P到達AC的中點時，點Q到達BC的中點時，S△OPQ=
S△ABC，
結束時，S△OPQ=S△BOC=
S△ABC，
所以，圖中陰影部分面積的大小變化情況是：先減小后增大．
故選C．
“點睛“本題考查了動點問題的函數圖象，根據題意找出關鍵的開始時，中點時，結束時三個時間點的三角形的面積與△ABC的面積的關系是解題的關鍵．
狀元及第系列答案
同步奧數系列答案科目：初中數學 來源： 題型：
【題目】要在一塊長52 m，寬48 m的矩形綠地上，修建同樣寬的兩條互相垂直的甬路，下面分別是小亮和小穎的設計方案．
(1)求小亮設計方案中甬路的寬度x；
(2)求小穎設計方案中四塊綠地的總面積．(友情提示：小穎設計方案中的x與小亮設計方案中的x取值相同)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】數學課上,老師出了一道題:化簡
[8(a+b)5-4(a+b)4+(-a-b)3]÷[2(a+b)3].
小明同學馬上舉手,下面是小明的解題過程:
[8(a+b)5-4(a+b)4+(-a-b)3]÷[2(a+b)3]
=[8(a+b)5-4(a+b)4+(a+b)3]÷8(a+b)3
=(a+b)2-
(a+b)+ 
.
小亮也舉起了手,說小明的解題過程不對,并指了出來.老師肯定了小亮的回答.你知道小明錯在哪兒嗎?請指出來,并寫出正確解答.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖
，已知等腰
在平面直角坐標系中，頂點
在
軸上，直角頂點
在
軸上，點
的坐標為
，直線
的解析式為
．
（
）求直線
的函數解析式．
（
）如圖
，直線
交
軸于
，延長
至點
，使
，連結
，求證： 
．
（
）如圖
，直線
交
軸于
，已知點
的坐標為
，在直線
上是否存在一點
，使
的面積是
面積的
，若存在，請求出點
的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】學校準備購進一批節能燈，已知1只A型節能燈和3只B型節能燈共需26元；3只A型節能燈和2只B型節能燈共需29元.
（1）求一只A型節能燈和一只B型節能燈的售價各是多少元；
（2）學校準備購進這兩種型號的節能燈共50只，并且A型節能燈的數量不多于B型節能燈數量的3倍，問A型節能燈最多可以買多少只？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD中，AB∥CD，過點D作DF⊥BC，垂足為F，DF與AC交于點M，已知∠1=∠2.
(1)求證：CM=DM；
(2)若FB=FC,求證：AM-MD=2FM.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com