【題目】濠河成功晉升國家
級旅游景區，為了保護這條美麗的護城河，南通市政府投入大量資金治理濠河污染，在城郊建立了一個大型污水處理廠，設庫池中有待處理的污水
噸，又從城區流入庫池的污水按每小時
噸的固定流量增加，如果同時開動
臺機組需
小時剛好處理完污水，同時開動
臺機組需
小時剛好處理完污水，若需要
小時內將污水處理完畢，那么至少要同時開動多少臺機組？（每臺機組每小時處理污水量不變）
科目：初中數學 來源： 題型：
【題目】如圖，△ABC的頂點坐標分別為A(1，3)、B(4，2)、C(2，1)．
(1)作出與△ABC關于x軸對稱的△A1B1C1，并寫出A1、B1、C1的坐標；
(2)以原點O為位似中心，在原點的另一側畫出△A2B2C2，使
．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】長沙市馬王堆蔬菜批發市場某批發商原計劃以每千克10元的單價對外批發銷售某種蔬菜
為了加快銷售，該批發商對價格進行兩次下調后，售價降為每千克
元．
求平均每次下調的百分率；
某大型超市準備到該批發商處購買2噸該蔬菜，因數量較多，該批發商決定再給予兩種優惠方案以供選擇方案一：打八折銷售；方案二：不打折，每噸優惠現金1000元試問超市采購員選擇哪種方案更優惠？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在8×8的正方形網格中，每個小正方形的邊長都為1，網格中有一個格點△ABC（即三角形的頂點都在格點上）.
（1）在圖中作出△ABC關于直線l對稱的△A1B1C1；（要求：A與A1，B與B1，C與C1相對應）
（2）
是 三角形；
（3）若有一格點P到點A、B的距離相等（PA=PB），則網格中滿足條件的點P共有 個；
(4)在直線
上找一點Q，使QB+QC的值最小。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，把矩形紙片ABCD沿對角線折疊，設重疊部分為△EBD，那么下列說法錯誤的是（ ）
A. △EBD是等腰三角形，EB=ED B. 折疊后∠ABE和∠C′BD一定相等
C. 折疊后得到的圖形是軸對稱圖形 D. △EBA和△EDC′一定是全等三角形
查看答案和解析>>
科目：初中數學 來源： 題型：
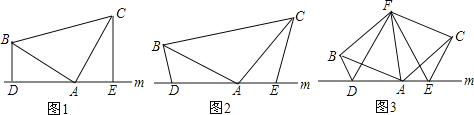
【題目】(1)如圖1，已知：在△ABC中，∠BAC=90°，AB=AC，直線m經過點A，BD⊥直線m，CE⊥直線m，垂足分別為點D、E．猜測DE、BD、CE三條線段之間的數量關系(直接寫出結果即可)．
(2)如圖2，將(1)中的條件改為：在△ABC中，AB=AC，D、A、E三點都在直線m上，并且有∠BDA=∠AEC=∠BAC=α，其中α為任意銳角或鈍角．請問第(1)題中DE、BD、CE之間的關系是否仍然成立？如成立，請你給出證明；若不成立，請說明理由．
(3)拓展與應用：如圖3，D、E是D、A、E三點所在直線m上的兩動點(D、A、E三點互不重合)，點F為∠BAC平分線上的一點，且△ABF和△ACF均為等邊三角形，連接BD、CE，若∠BDA=∠AEC=∠BAC，試判斷線段DF、EF的數量關系，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示,已知△ABC和△DCE均是等邊三角形,點B. C. E在同一條直線上,AE與BD交于點O,AE與CD交于點G,AC與BD交于點F,連接OC、FG,則下列結論中：①AE=BD;②AG=BF;③FG∥BE；④∠BOC=∠EOC，正確的是（ ）個
A.1B.2C.3D.4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，∠C=90°，D是AC的中點，E是AB的中點，作EF⊥BC于F，延長BC至G，使CG=BF，連接CE、DE、DG．
（1）如圖1，求證：四邊形CEDG是平行四邊形；
（2）如圖2，連接EG交AC于點H，若EG⊥AB，請直接寫出圖2中所有長度等于
GH的線段．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，在四邊形ABCD中，AD∥BC，M為CD中點，AM平分∠DAB，AD＋BC＝AB．求證：BM平分∠ABC．
小淇證明過程如下：
延長BC至點F，使得CF＝AD，連接MF．
∵ AD∥BC， ∴ ∠D＝∠MCF．
∵ M為CD中點，∴ DM＝CM．
在△ADM和△FCM中，
∴ △ADM≌△FCM（SAS）． ∴ AM＝FM．
∵ BF＝BC＋CF＝BC＋AD＝AB，∴ △ABF是等腰三角形．
∴ BM平分∠ABC（等腰三角形底邊上的中線與頂角的角平分重合）．
（1）請你簡要敘述小淇證明方法的錯誤之處；
（2）若AB＝5，AM＝3，求四邊形ABCD面積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
