Question

【題目】如圖，己知直線l1l2，且l3和l1，l2分別交于A、B兩點，點P在直線AB上

試找出之間的關系并說明理由；

當點P在A，B兩點間運動時，問之間的關系是否發生變化？

如果點P在A，B兩點外側運動時，試探究之間的關系只寫結論，不需要說明理由，并在備用圖①、②中畫出對應圖形．

Answer 1

【答案】（1）∠1+∠2=∠3；不發生變化；（3）∠1-∠2=∠3或∠2-∠1=∠3；；

【解析】試題分析：（1）過點P作l1的平行線，根據平行線的性質即可解決問題．（2）（3）類比（1）的方法解決即可．

試題解析：

（1）∠1+∠2=∠3；

理由：如圖，過點P作l1的平行線，

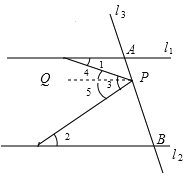
∵l1∥l2，

∴l1∥l2∥PQ，

∴∠1=∠4，∠2=∠5，（兩直線平行，內錯角相等）

∵∠4+∠5=∠3，

∴∠1+∠2=∠3；

（2）同（1）可證：∠1+∠2=∠3；

（3）∠1-∠2=∠3或∠2-∠1=∠3

理由：當點P在下側時，過點P作l1的平行線PQ，

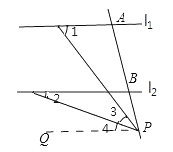
∵l1∥l2，

∴l1∥l2∥PQ，

∴∠2=∠4，∠1=∠3+∠4，（兩直線平行，內錯角相等）

∴∠1-∠2=∠3；

當點P在上側時，同理可得：∠2-∠1=∠3．