
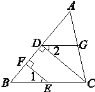
【題目】如圖所示,在△ABC中,E,G分別是BC,AC上的點,D,F是AB上的點,已知EF⊥AB,垂足為F,CD⊥AB,垂足為D,∠1=∠2, 試判斷∠AGD和∠ACB是否相等,為什么?
【答案】∠AGD=∠ACB,理由見解析.
【解析】
根據垂直的定義得到∠BFE=∠BDC=90°,根據平行線的判定方法得到EF∥CD,則∠1=∠ECD,由于∠1=∠2,則∠2=∠ECD,于是可根據平行線的判定方法得到DG∥BC,然后根據平行線的性質即可得到∠AGD=∠ACB.
∠AGD=∠ACB.
理由如下:
因為EF⊥AB,CD⊥AB(已知),所以∠EFB=∠CDB=90°(垂直的定義),
所以EF∥CD(同位角相等,兩直線平行),所以∠1=∠ECD(兩直線平行,同位角相等).又因為∠1=∠2(已知),所以∠ECD=∠2(等量代換),所以GD∥CB(內錯角相等,兩直線平行),所以∠AGD=∠ACB(兩直線平行,同位角相等).


 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,CO⊥AB于點O,CD是⊙O的切線,切點為D.連接BD,交OC于點E. 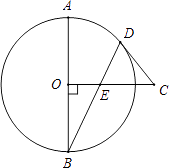
(1)求證:∠CDE=∠CED;
(2)若AB=13,BD=12,求DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①是一個長為2m、寬為2n的長方形,沿圖中虛線用剪刀將其均勻分成四個小長方形,然后按圖②的形狀拼成一個正方形.
(1)你認為圖②中陰影部分的正方形的邊長等于________;
(2)請你用兩種不同的方法表示圖②中陰影部分的面積,方法一:__________________,方法二:________________;
(3)觀察圖②,你能寫出代數式(m+n)2,(m-n)2,mn之間的關系嗎?
(4)應用:已知m+n=11,mn=28(m>n),求m,n的值.
 ①
①  ②
②
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC的AC邊在直線m上,∠ACB=80°,以C為圓心, ![]() BC長為半徑畫弧,交直線m于點D1、交BC于點E1 , 連接D1E1;又以D1為圓心,
BC長為半徑畫弧,交直線m于點D1、交BC于點E1 , 連接D1E1;又以D1為圓心, ![]() D1E1長為半徑畫弧,交直線m于點D2、交D1E1于點E2 , 連接D2E2;又以D2為圓心,
D1E1長為半徑畫弧,交直線m于點D2、交D1E1于點E2 , 連接D2E2;又以D2為圓心, ![]() D2E2長為半徑畫弧,交直線m于點D3、交D2E2于點E3 , 連接D3E3;如此依次下去,…,第n次時所得的∠EnDnDn﹣1= .
D2E2長為半徑畫弧,交直線m于點D3、交D2E2于點E3 , 連接D3E3;如此依次下去,…,第n次時所得的∠EnDnDn﹣1= . 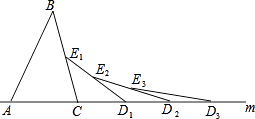
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AD>AB,將矩形ABCD折疊,使點C與點A重合,折痕為MN,連接CN.若△CDN的面積與△CMN的面積比為1:4,則 ![]() 的值為( )
的值為( ) 
A.2
B.4
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)某地區為了鼓勵市民節約用水,計劃實行生活用水按階梯式水價計費,每月用水量不超過10噸(含10噸)時,每噸按基礎價收費;每月用水量超過10噸時,超過的部分每噸按調節價收費.例如,第一個月用水16噸,需交水費17.8元,第二個月用水20噸,需交水費23元.
(1)求每噸水的基礎價和調節價;
(2)設每月用水量為n噸,應交水費為m元,寫出m與n之間的函數解析式;
(3)若某月用水12噸,應交水費多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com