
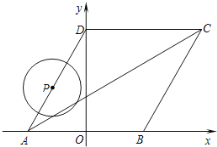
【題目】如圖所示,菱形ABCD的頂點A、B在![]() 軸上,點A在點B的左側,點D在
軸上,點A在點B的左側,點D在![]() 軸的正半軸上,
軸的正半軸上,![]() ,點A的坐標為
,點A的坐標為![]() .
.
(1)求D點的坐標.
(2)求直線AC的函數關系式.
(3)動點P從點A出發,以每秒1個單位長度的速度,按照![]() 的順序在菱形的邊上勻速運動一周,設運動時間為
的順序在菱形的邊上勻速運動一周,設運動時間為![]() 秒.求
秒.求![]() 為何值時,以點P為圓心、以1為半徑的圓與對角線AC相切?
為何值時,以點P為圓心、以1為半徑的圓與對角線AC相切?
【答案】(1)(0,2![]() );(2)
);(2)![]() ;(3)t=2或6或10或14
;(3)t=2或6或10或14
【解析】
(1)在Rt△AOD中,根據OA的長以及∠BAD的正切值,即可求得OD的長,從而得到D點的坐標;
(2)根據點A、C的坐標,利用待定系數法可求得直線AD的解析式.
(3)由于點P沿菱形的四邊勻速運動一周,那么本題要分作四種情況考慮:
在Rt△OAD中,易求得AD的長,也就得到了菱形的邊長,而菱形的對角線平分一組對角,那么∠DAC=∠BAC=∠BCA=∠DCA=30°;
①當點P在線段AD上時,若⊙P與AC相切,由于∠PAC=30°,那么AP=2R(R為⊙P的半徑),由此可求得AP的長,即可得到t的值;
②③④的解題思路與①完全相同,只不過在求t值時,方法略有不同.
解:(1)∵點A的坐標為(-2,0),∠BAD=60°,∠AOD=90°,
∴OD=OAtan60°=2![]() ,AD=4,
,AD=4,
∴點D的坐標為(0,2![]() );
);
(2)根據(1)知點D的坐標為(0,2![]() )
)
∵AD=CD,CD∥AB,
∴C(4,2![]() );
);
設直線AC的函數表達式為y=kx+b(k≠0),
∵A(-2,0),C(4,2![]() ),
),
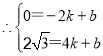
解得: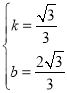
∴直線AC的解析式為![]() ;
;
(3)∵四邊形ABCD是菱形,
∴∠DCB=∠BAD=60°,
∴∠1=∠2=∠3=∠4=30°,
AD=DC=CB=BA=4,
如圖所示:
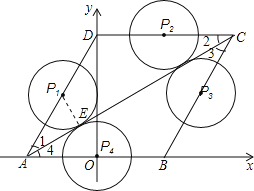
①點P在AD上與AC相切時,
連接P1E,則P1E⊥AC,P1E=r,
∵∠1=30°,
∴AP1=2r=2,
∴t1=2.
②點P在DC上與AC相切時,
CP2=2r=2,
∴AD+DP2=6,
∴t2=6.
③點P在BC上與AC相切時,
CP3=2r=2,
∴AD+DC+CP3=10,
∴t3=10.
④點P在AB上與AC相切時,
AP4=2r=2,
∴AD+DC+CB+BP4=14,
∴t4=14,
∴當t=2或6或10或14時,以點P為圓心、以1為半徑的圓與對角線AC相切.
故答案為:(1)(0,2![]() );(2)
);(2)![]() ;(3)t=2或6或10或14.
;(3)t=2或6或10或14.


科目:初中數學 來源: 題型:
【題目】某公司開發處一款新的節能產品,該產品的成本價為6元/件,該產品在正式投放市場前通過代銷點進行了為期一個月(30天)的試銷售,售價為10元/件,工作人員對銷售情況進行了跟蹤記錄,并將記錄情況繪制成圖象,圖中的折線ABC表示日銷售量y(件)與銷售時間x(天)之間的函數關系.

(1)求y與x之間的函數表達式,并寫出x的取值范圍;
(2)若該節能產品的日銷售利潤為W(元),求W與x之間的函數表達式,并求出日銷售利潤不超過1040元的天數共有多少天?
(3)若5≤x≤17,直接寫出第幾天的日銷售利潤最大,最大日銷售利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,四邊形![]() 內接于⊙
內接于⊙![]() ,
,![]() 是⊙
是⊙![]() 的直徑,過點
的直徑,過點![]() 的切線與
的切線與![]() 的延長線相交于點
的延長線相交于點![]() .且
.且![]() ,連接
,連接![]() .
.

(1)求證:![]() ;
;
(2)過點![]() 作
作![]() ,垂足為
,垂足為![]() ,當
,當![]() 時,求⊙
時,求⊙![]() 的半徑;
的半徑;
(3)在(2)的條件下,求陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一個圓形轉盤,分黑色、白色兩個區域.
(1)某人轉動轉盤,對指針落在黑色區域或白色區域進行了大量試驗,得到數據如下表:
實驗次數 | 10 | 100 | 2000 | 5000 | 10000 | 50000 | 100000 |
白色區域次數 | 3 | 34 | 680 | 1600 | 3405 | 16500 | 33000 |
落在白色區域頻率 | 0.3 | 0.34 | 0.34 | 0.32 | 0.34 | 0.33 | 0.33 |
請你利用上述實驗,估計轉動該轉盤指針落在白色區域的概率為___________.(精確到0.01);
(2)若該圓形轉盤白色扇形的圓心角為120度,黑色扇形的圓心角為![]() ,轉動轉盤兩次,求指針一次落在白色區域,另一次落在黑色區域的概率.
,轉動轉盤兩次,求指針一次落在白色區域,另一次落在黑色區域的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,弦
的直徑,弦![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 的切線交
的切線交![]() 的延長線于點
的延長線于點![]() .
.
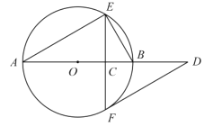
(1)已知![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(2)取![]() 的中點
的中點![]() ,連接
,連接![]() ,請補全圖形;若
,請補全圖形;若![]() ,
,![]() ,求
,求![]() 的半徑.
的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
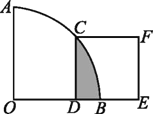
【題目】如圖,在扇形AOB中,∠AOB=90°,正方形CDEF的頂點C是![]() 的中點,點D在OB上,點E在OB的延長線上,當正方形CDEF的邊長為2
的中點,點D在OB上,點E在OB的延長線上,當正方形CDEF的邊長為2![]() 時,陰影部分的面積為________
時,陰影部分的面積為________
查看答案和解析>>
科目:初中數學 來源: 題型:
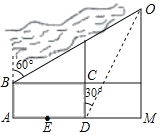
【題目】如圖所示,小亮家在點O處,其所在學校的校園為矩形ABCD,東西長AD=1000米,南北長AB=600米.學校的南正門在AD的中點E處,B為學校的西北角門.小亮從家到學校可以走馬路,路線O→M→E(∠M=90°);也可以走沿河觀光路,路線O→B.小亮在D處測得O位于北偏東30°,在B處測得O位于北偏東60°小亮從家到學校的兩條路線中,長路線比短路線多_____米.(結果保留根號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com