
���}Ŀ����D��CD��AB���c(di��n)D���c(di��n)E��CD�ϣ������Ă�(g��)�l������AD��ED������A����BED������C����B����AC��EB�������Ѓɂ�(g��)����l���������ж���ADC�ա�EDB����

A.�٢�B.�٢�C.�ڢ�D.�ڢ�
���𰸡�C
��������
����(j��)ȫ�������ε��ж������Լ�ֱ��������ȫ���ж����������M(j��n)���Д༴�ɡ�
A����CD��AB
���CDA=��BDE
�֡�AD��ED������A����BED
���ADC�ա�EDB��ASA��
����A���Д����ȫ�ȣ�
B����CD��AB
���ADC�c��EDB��ֱ��������
��AD=ED,AC=EB
���ADC�ա�EDB��HL��
����B���Д����ȫ�ȣ�
C������(j��)����(g��)����(y��ng)����ȟo���Д��ɂ�(g��)������ȫ�ȣ�
����C�����Д����ȫ�ȣ�
D����CD��AB
���CDA=��BDE
�֡ߡ�A����BED��AC��EB
���ADC�ա�EDB��AAS��
����D���Д����ȫ�ȣ�
���Դ𰸞�C�x�(xi��ng)��



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����![]() �;���
�;���![]() ��
��

��1����Ҫ�����D(�����������E����������)��
���L����![]() ���c(di��n)
���c(di��n)![]() ��ʹ
��ʹ![]() ���������L����
���������L����![]() ���c(di��n)
���c(di��n)![]() ��ʹ
��ʹ![]() ��
��
��2�����![]() ��
��![]() �քe�Ǿ���
�քe�Ǿ���![]() ��
��![]() �����c(di��n)����
�����c(di��n)����![]() ��
��![]() ����
����![]() ���L��
���L��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��![]() ��(j��ng)�^
��(j��ng)�^![]() ��c(di��n)
��c(di��n)![]() ��һ�lֱ����
��һ�lֱ����![]() ��
��![]() �քe��ֱ��
�քe��ֱ��![]() �σ��c(di��n)����
�σ��c(di��n)����![]() ��
��
��1����ֱ��![]() ��(j��ng)�^
��(j��ng)�^![]() �ă�(n��i)������
�ă�(n��i)������![]() ���侀
���侀![]() �ϣ�Ո��Q����ɂ�(g��)���}��
�ϣ�Ո��Q����ɂ�(g��)���}��
����D1����![]() ��
��![]() ��
��
�t![]()
![]() ��
��![]()
![]() ������
������![]() ������
������![]() ������
������![]() ������
������
����D2����![]() ��Ո?zh��)���һ��(g��)�P(gu��n)��
��Ո?zh��)���һ��(g��)�P(gu��n)��![]() �c
�c![]() �P(gu��n)ϵ�ėl�� ��ʹ���еăɂ�(g��)�Y(ji��)Փ��Ȼ���������C���ɂ�(g��)�Y(ji��)Փ������
�P(gu��n)ϵ�ėl�� ��ʹ���еăɂ�(g��)�Y(ji��)Փ��Ȼ���������C���ɂ�(g��)�Y(ji��)Փ������
��2����D3����ֱ��![]() ��(j��ng)�^
��(j��ng)�^![]() ���ⲿ��
���ⲿ��![]() ��Ո?zh��)�?/span>
��Ո?zh��)�?/span>![]() ���l���Δ�(sh��)���P(gu��n)ϵ�ĺ������루��Ҫ���C������
���l���Δ�(sh��)���P(gu��n)ϵ�ĺ������루��Ҫ���C������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D������![]() �У�
��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ��
��![]() ߅��һ�c(di��n)���B��
߅��һ�c(di��n)���B��![]() ����
����![]() ��
��![]() �ۯB��ʹ�c(di��n)
�ۯB��ʹ�c(di��n)![]() �����c(di��n)
�����c(di��n)![]() ̎.��(d��ng)
̎.��(d��ng)![]() ��ֱ�������Εr(sh��)���t
��ֱ�������Εr(sh��)���t![]() ���L��________.
���L��________.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������˾��Ą�(l��)����(ji��)�s��늣���ȡ����������ֶ����M(f��i)�k������ij������ÿ��(y��ng)����M(f��i)y��Ԫ���c�����x���ȣ��ĺ���(sh��)�D����һ�l�۾�����D��ʾ��������(j��)�D������І��}��
(1) �քe������(d��ng)0��x��100��x��100�r(sh��)��y�cx�ĺ���(sh��)�P(gu��n)ϵʽ
(2) ���ú���(sh��)�P(gu��n)ϵʽ���f�������˾��ȡ�����M(f��i)��(bi��o)��(zh��n)
(3) ��ԓ�Ñ�ij�����62�ȣ��t��(y��ng)�U�M(f��i)����Ԫ����ԓ�Ñ�ij���U�M(f��i)105Ԫ�r(sh��)���tԓ�Ñ�ԓ�����˶��ٶ�늣�

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D�ǹ��ˎ�����ͬһ�N�����ƳɵĽ��ٿ�ܣ���֪��B����E��AB��DE��BF��EC��������ABC�����L��24cm��CF��3cm���t�Ƴ�����(g��)���ٿ�������@�N���ϵĿ��L�Ȟ� ________cm.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����ƽ��ֱ������(bi��o)ϵ�У�ֱ��![]() �քe�c
�քe�c![]() �S��
�S��![]() �S�����c(di��n)
�S�����c(di��n)![]() ��
��![]() �����c(di��n)
�����c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ���c(di��n)
���c(di��n)![]() ��
��![]() �����c(di��n).
�����c(di��n).
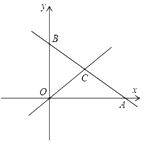
��1���c(di��n)![]() ������(bi��o)��________���c(di��n)
������(bi��o)��________���c(di��n)![]() ������(bi��o)��________;
������(bi��o)��________;
��2��ֱ��![]() ����һ�c(di��n)
����һ�c(di��n)![]() ����
����![]() ��ԇ����c(di��n)
��ԇ����c(di��n)![]() ������(bi��o)��
������(bi��o)��
��3�����c(di��n)![]() ��ֱ��
��ֱ��![]() �ϵ�һ��(g��)��(d��ng)�c(di��n)���^�c(di��n)
�ϵ�һ��(g��)��(d��ng)�c(di��n)���^�c(di��n)![]() ��
��![]() �S�Ĵ������cֱ��
�S�Ĵ������cֱ��![]() �����c(di��n)
�����c(di��n)![]() ���O(sh��)�c(di��n)
���O(sh��)�c(di��n)![]() �ęM����(bi��o)��
�ęM����(bi��o)��![]() ������
������![]() ���L�Ȟ�
���L�Ȟ�![]() ����
����![]() �c
�c![]() �ĺ���(sh��)����ʽ.
�ĺ���(sh��)����ʽ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
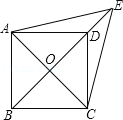
���}Ŀ����D����֪ƽ����߅��ABCD�У����Ǿ�AC��BD�����c(di��n)O��E��BD���L���ϵ��c(di��n)���ҡ�ACE�ǵ�߅�����Σ�
��1�����C����߅��ABCD�����Σ�
��2������AED=2��EAD�����C����߅��ABCD�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����߅�L��2��������ABCD�У��c(di��n)P��߅AD�ϵĄ�(d��ng)�c(di��n)���c(di��n)P���c�c(di��n)A���c(di��n)D�غϣ����c(di��n)Q��߅CD��һ�c(di��n)���B��PB��PQ������PBC����BPQ��
�� ��tan��PBC=4����AP���L��
�� �Ƿ�����c(di��n)P��ʹ���c(di��n)Qǡ����߅CD�����c(di��n)�������ڣ����AP���L���������ڣ�Ո�f�����ɣ��� �B��BQ������PBQ���Ƿ���ڶȔ�(sh��)��׃�Ľǣ������ڣ�ָ���@��(g��)�ǣ���������ĶȔ�(sh��)���������ڣ�Ո�f�����ɣ�

�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com