
【題目】已知A,B,C三點在數軸上的位置如圖所示,它們表示的數分別是a,b,c.
(1)填空:abc 0,a+b 0,ab﹣ac 0;(填“>”,“=”或“<”)
(2)若|a|=2且點B到點A,C的距離相等,
①當b2=16時,求c的值;
②P是數軸上B,C兩點之間的一個動點,設點P表示的數為x,當P點在運動過程中,bx+cx+|x﹣c|﹣10|x+a|的值保持不變,求b的值.
![]()
【答案】(1)<,>,>;(2)①10,②3
【解析】
(1)根據點在數軸上的位置得到a<0<b<c,|b|>|a|,于是得到結論;
(2)①根據已知條件達到a=﹣2,b=4,根據點B到點A,C的距離相等,列方程即可得到結論;
②依題意得原式=(b+c﹣11)x+10a+c當P點在運動過程中,原式的值保持不變,即原式的值與x無關,列方程組即可得到結論.
解:(1)∵a<0<b<c,|b|>|a|,
∴abc<0,a+b>0,ab﹣ac>0,
故答案為:<,>,>;
(2)①∵|a|=2 且a<0,
∴a=﹣2,
∵b2=16 且b>0,
∴b=4,
∵點B到點A,C的距離相等,
∴|4﹣(﹣2)|=|c﹣4|,
∴c=10;
②依題意,得bx+cx+|x﹣c|﹣10|x+a|=bx+cx+c﹣x﹣10x﹣10a=(b+c﹣11)x﹣10a+c,
∴原式=(b+c﹣11)x﹣10a+c
∵當P點在運動過程中,原式的值保持不變,
即原式的值與x無關,
∴b+c﹣11=0,
又∵b+2=c﹣b,
∴b=3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,BE、CE分別平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.則ABCD的周長為_____,面積為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一副三角板中的兩塊直角三角尺的直角頂點C按如圖方式疊放在一起(其中∠A=60°,∠D=30°,∠E=∠B=45°).
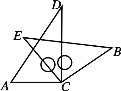
(1)猜想∠ACB與∠DCE的數量關系,并說明理由.
(2)當∠ACE<180°且點E在直線AC的上方時,這兩塊三角尺是否存在一組邊互相平行?若存在,請直接寫出∠ACE所有可能的度數及對應情況下的平行線(不必說明理由);若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(11分)如圖,四邊形ABCD為菱形,點E為對角線AC上的一個動點,連結DE并延長交AB于點F,連結BE.
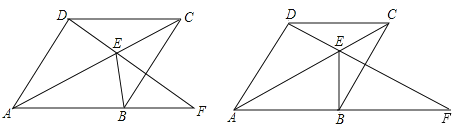
(1)如圖①,求證:∠AFD=∠EBC;
(2)如圖②,若DE=EC且BE⊥AF,求∠DAB的度數;
(3)若∠DAB=90°且當△BEF為等腰三角形時,求∠EFB的度數(只寫出條件與對應的結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】剛剛升入初一,學習成績優異但體育一般的王晴同學未雨綢繆,已經為將來的體育中考做起了準備.上周末她在家練習1分鐘跳繩,以每分鐘150下為基準,超過或不足的部分分別用正負數來表示,8次成績(單位:下)分別是-10,-8,-5,-2,+2,+8,+3,-4.
(1)成績最好的一次比最差的一次多跳多少下?
(2)求王晴這8次跳繩的平均成績.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在一次大課間活動中,采用了四鐘活動形式:A、跑步,B、跳繩,C、做操,D、游戲.全校學生都選擇了一種形式參與活動,小杰對同學們選用的活動形式進行了隨機抽樣調查,根據調查統計結果,繪制了不完整的統計圖.


請結合統計圖,回答下列問題:
(1)本次調查學生共 人, ![]() = ,并將條形圖補充完整;
= ,并將條形圖補充完整;
(2)如果該校有學生2000人,請你估計該校選擇“跑步”這種活動的學生約有多少人?
(3)學校讓每班在A、B、C、D四鐘活動形式中,隨機抽取兩種開展活動,請用樹狀圖或列表的方法,求每班抽取的兩種形式恰好是“跑步”和“跳繩”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,甲、乙兩人以相同路線前往離學校12千米的地方參加植樹活動.分析甲、乙兩人前往目的地所行駛的路程S(千米)隨時間t(分鐘)變化的函數圖象,解決下列問題:

(1)求出甲、乙兩人所行駛的路程S甲、S乙與t之間的關系式;
(2)甲行駛15分鐘后,甲、乙兩人相距多少千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明同學為了解自己居住的小區家庭生活用水情況,從中隨機調查了其中![]() 的家庭一年的月平均用水量(單位:頓).并將調查結果制成了如圖所示的條形和扇形統計圖.
的家庭一年的月平均用水量(單位:頓).并將調查結果制成了如圖所示的條形和扇形統計圖.
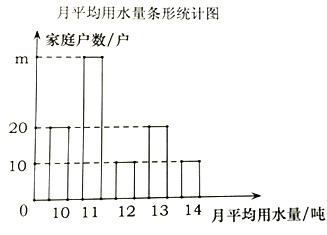
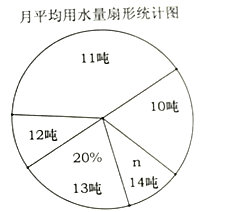
![]() 小明隨機調查了 戶家庭,該小區共有 戶家庭;
小明隨機調查了 戶家庭,該小區共有 戶家庭;
![]()
![]() ,
,![]() ;
;
![]() 這個樣本數據的眾數是 ,中位數是 ;
這個樣本數據的眾數是 ,中位數是 ;
![]() 根據樣本數據,請估計該小區家庭月平均用水量不超過
根據樣本數據,請估計該小區家庭月平均用水量不超過![]() 噸的有多少戶?
噸的有多少戶?
查看答案和解析>>
科目:初中數學 來源: 題型:
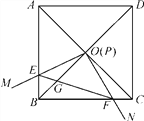
【題目】如圖,邊長為1的正方形ABCD的對角線AC,BD相交于點O,有直角∠MPN,使直角頂點P與點O重合,直角邊PM,PN分別與OA,OB重合,然后逆時針旋轉∠MPN,旋轉角為θ(0°<θ<90°),PM,PN分別交AB,BC于E,F兩點,連接EF交OB于點G,則下列結論:(1)EF=![]() OE;(2)S四邊形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=
OE;(2)S四邊形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=![]() OA;(4)在旋轉過程中,當△BEF與△COF的面積之和最大時,AE=
OA;(4)在旋轉過程中,當△BEF與△COF的面積之和最大時,AE=![]() ;(5)OG·BD=AE2+CF2,其中正確的是__.
;(5)OG·BD=AE2+CF2,其中正確的是__.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com