【題目】已知
是
的直徑，
，
、
分別與圓相交于
、
，那么下列等式中一定成立的是（ ）
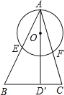
A. AEBF=AFCF B. AEAB=AOAD'
C. AEAB=AFAC D. AEAF=AOAD
閱讀快車系列答案科目：初中數(shù)學(xué) 來源： 題型：
【題目】某校為了解本校學(xué)生每周參加課外輔導(dǎo)班的情況，隨機調(diào)査了部分學(xué)生一周內(nèi)參加課外輔導(dǎo)班的學(xué)科數(shù)，并將調(diào)查結(jié)果繪制成如圖1、圖2所示的兩幅不完整統(tǒng)計圖（其中A：0個學(xué)科，B：1個學(xué)科，C：2個學(xué)科，D：3個學(xué)科，E：4個學(xué)科或以上），請根據(jù)統(tǒng)計圖中的信息，解答下列問題：
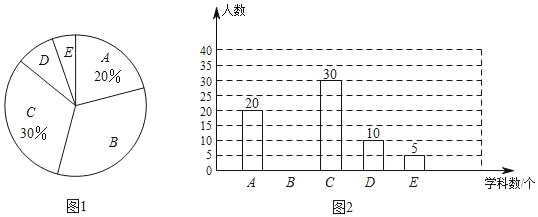
（1）請將圖2的統(tǒng)計圖補充完整；
（2）根據(jù)本次調(diào)查的數(shù)據(jù)，每周參加課外輔導(dǎo)班的學(xué)科數(shù)的眾數(shù)是 個學(xué)科；
（3）若該校共有2000名學(xué)生，根據(jù)以上調(diào)查結(jié)果估計該校全體學(xué)生一周內(nèi)參加課外輔導(dǎo)班在3個學(xué)科（含3個學(xué)科）以上的學(xué)生共有 人．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
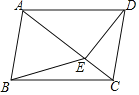
【題目】如圖，在四邊形ABCD中，AB∥CD，∠ABC＝∠ADC，DE垂直于對角線AC，垂足是E，連接BE．
（1）求證：四邊形ABCD是平行四邊形；
（2）若△ABE是等邊三角形，四邊形BCDE的面積等于2
，求CE的長．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
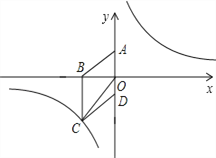
【題目】如圖，在平面直角坐標(biāo)系中，已知四邊形ABCD為菱形，且
（0，3）、
（﹣4，0）．
（1）求經(jīng)過點
的反比例函數(shù)的解析式；
（2）設(shè)
是（1）中所求函數(shù)圖象上一點，以
頂點的三角形的面積與△COD的面積相等．求點P的坐標(biāo)．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如果一個三角形的兩條邊的和是第三邊的兩倍，則稱這個三角形是“優(yōu)三角形”，這兩條邊的比稱為“優(yōu)比”（若這兩邊不等，則優(yōu)比為較大邊與較小邊的比），記為
.
（1）命題：“等邊三角形為優(yōu)三角形，其優(yōu)比為1”，是真命題還是假命題？
（2）已知
為優(yōu)三角形，
，
，
，
①如圖1，若
，
，
，求
的值.
②如圖2，若
，求優(yōu)比的取值范圍.
（3）已知是優(yōu)三角形，且
，
，求的面積.
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】對于一元二次方程
，下列說法：①若
，則方程必有一根為
；②若
是方程的一個根，則一定有
成立；③若
，則方程一定有兩個不相等實數(shù)根；其中正確結(jié)論有（ ）個．
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
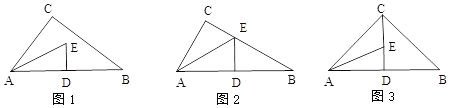
【題目】如圖1，△ABC是直角三角形，∠C=90°，∠CAB的角平分線AE與 AB的垂直平分線DE相交于點E.
（1）如圖2，若點E正好落在邊BC上.
①求∠B的度數(shù)
②證明：BC=3DE
（2）如圖3，若點E滿足C、E、D共線.
求證：AD+DE=BC.
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
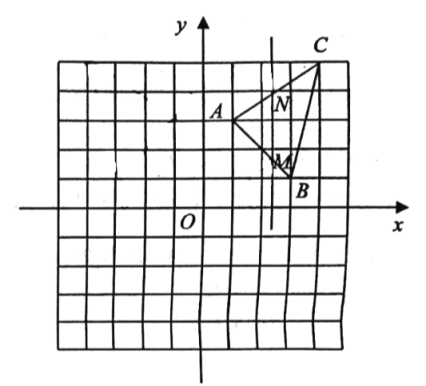
【題目】如圖，在平面直角坐標(biāo)系中，點
，點
，點
.
（1）畫出
關(guān)于
軸的對稱圖形
，并寫出點
的對稱點
的坐標(biāo)；
（2）若點
在
軸上，連接
、
，則
的最小值是 ；
（3）若直線
軸，與線段
、
分別交于點
、
（點不與點重合），若將
沿直線
翻折，點的對稱點為點
，當(dāng)點落在的內(nèi)部（包含邊界）時，點的橫坐標(biāo)
的取值范圍是 .
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
