Question

【題目】如果一個三角形的三邊a，b，c能滿足a2+b2=nc2（n為正整數），那么這個三角形叫做“n階三角形”．如三邊分別為1、2、的三角形滿足12+22=1×（）2，所以它是1階三角形，但同時也滿足（）2+22=9×12，所以它也是9階三角形．顯然，等邊三角形是2階三角形，但2階三角形不一定是等邊三角形．

（1）在我們熟知的三角形中，何種三角形一定是3階三角形？

（2）若三邊分別是a，b，c（a＜b＜c）的直角三角形是一個2階三角形，求a：b：c．

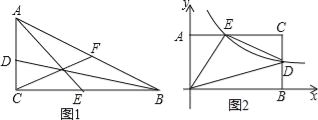
（3）如圖1，直角△ABC是2階三角形，AC＜BC＜AB，三條中線BD、AE、CF所構成的三角形是何種三角形？四位同學作了猜想：

A同學：是2階三角形但不是直角三角形；

B同學：是直角三角形但不是2階三角形；

C同學：既是2階三角形又是直角三角形；

D同學：既不是2階三角形也不是直角三角形．

請你判斷哪位同學猜想正確，并證明你的判斷．

（4）如圖2，矩形OACB中，O為坐標原點，A在y軸上，B在x軸上，C點坐標是（2，1），反比例函數y=（k＞0）的圖象與直線AC、直線BC交于點E、D，若△ODE是5階三角形，直接寫出所有可能的k的值．

Answer 1

【答案】（1）等腰直角三角形一定是3階三角形，（2）a：b：c=1：：；（3）C同學猜想正確，（4）滿足題意k的值為1，4，7，．

【解析】

試題分析：（1）等腰直角三角形為3階三角形，根據題中的新定義驗證即可；

（2）根據題中的新定義列出關系式，再利用勾股定理列出關系式，即可確定出a，b，c的比值；

（3）C同學猜想正確，由直角△ABC是2階三角形，根據（2）中的結論得出AC，BC，AB之比，設出三邊，表示出AE，BD，CF，利用題中的新定義判斷即可；

（4）根據圖形設出E與D坐標，利用勾股定理表示出OE2，OD2以及ED2，由△ODE是5階三角形，分類討論列出關于k的方程，求出方程的解即可得到k的值

試題解析：（1）等腰直角三角形一定是3階三角形，

理由為：設等腰直角三角形兩直角邊為a，a，

根據勾股定理得：斜邊為a，

則有a2+（a）2=3a2，即等腰直角三角形一定是3階三角形；

（2）∵△ABC為一個2階直角三角形，

∴c2=a2+b2，且c2+a2=2b2，

兩式聯立得：2a2+b2=2b2，

整理得：b=a，c=a，

則a：b：c=1：：；

（3）C同學猜想正確，

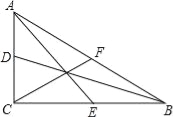
證明如下：如圖，∵△ABC為2階直角三角形，

∴AC：BC：AB=1：：，

設BC=2，AC=2，AB=2，

∵AE，BD，CF是Rt△ABC的三條中線，

∴AE2=6，BD2=9，CF2=3，

∴BD2+CF2=2AE2，AE2+CF2=BD2，

∴BD，AE，CF所構成的三角形既是直角三角形，又是2階三角形；

（4）根據題意設E（k，1），D（2，），

則AE=k，EC=2﹣k，BD=，CD=1﹣，OA=1，OB=2，

根據勾股定理得：OE2=1+k2，OD2=4+，ED2=（2﹣k）2+（1﹣）2，

由△ODE是5階三角形，分三種情況考慮：

當OE2+OD2=5ED2時，即1+k2+4+=5[（2﹣k）2+（1﹣）2]，

整理得：k2﹣5k+4=0，即（k﹣1）（k﹣4）=0，

解得：k=1或k=4；

當OE2+ED2=5OD2時，（2﹣k）2+（1﹣）2+1+k2=5（4+），

整理得：k2﹣5k﹣14=0，即（k﹣7）（k+2）=0，

解得：k=7或k=﹣2（舍去）；

當OD2+ED2=5OE2時，4++（2﹣k）2+（1﹣）2=5（1+k2），

整理得：7k2+10k﹣8=0，即（7k﹣4）（k+2）=0，

解得：k=或k=﹣2（舍去），

綜上，滿足題意k的值為1，4，7，．