【題目】計算：(﹣a2)3=( )
A. a6B. ﹣a6C. a5D. ﹣a5
字詞句篇與同步作文達標系列答案科目：初中數學 來源： 題型：
【題目】歷史上的數學巨人歐拉最先把關于x的多項式用記號f（x）的形式來表示（f可用其它字母，但不同的字母表示不同的多項式），例如f（x）=x2+3x﹣5，把x=某數時的多項式的值用f（某數）來表示．
例如x=﹣1時多項式x2+3x﹣5的值記為f（﹣1）=（﹣1）2+3×（﹣1）﹣5=﹣7，
已知g（x）=﹣2x2﹣3x+1，h（x）=ax3+2x2﹣x
（1）求g（﹣2）的值；
（2）若h（﹣2）=14，求g（a）的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC和△DCB中，∠A=∠D=90°，AC=BD，AC與BD相交于點O．
（1）求證：△ABO≌△DCO；
（2）△OBC是何種三角形？證明你的結論．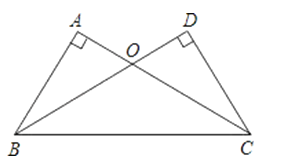
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校組織學生排球墊球訓練，訓練前后，對每個學生進行考核．現隨機抽取部分學生，統計了訓練前后兩次考核成績，并按“A，B，C”三個等次繪制了如圖不完整的統計圖．試根據統計圖信息,解答下列問題：
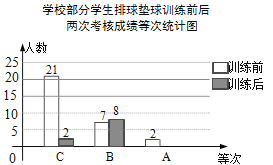
（1）抽取的學生中，訓練后“A”等次的人數是多少？并補全統計圖．
（2）若學校有600名學生，請估計該校訓練后成績為“A”等次的人數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】著名的瑞士數學家歐拉曾指出：可以表示為四個整數平方之和的甲、乙兩數相乘，其乘積仍然可以表示為四個整數平方之和，即 
，這就是著名的歐拉恒等式，有人稱這樣的數為“不變心的數”．實際上，上述結論可概括為：可以表示為兩個整數平方之和的甲、乙兩數相乘，其乘積仍然可以表示為兩個整數平方之和．
【閱讀思考】
在數學思想中，有種解題技巧稱之為“無中生有”．例如問題：將代數式 
改成兩個平方之差的形式．解：原式 
﹒
（1）【動手一試】試將 
改成兩個整數平方之和的形式． （12+52）（22+72）=；
（2）【解決問題】請你靈活運用利用上述思想來解決“不變心的數”問題：將代數式 
改成兩個整數平方之和的形式（其中a、b、c、d均為整數），并給出詳細的推導過程﹒
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
