
【題目】海水養(yǎng)殖是萊州經(jīng)濟產(chǎn)業(yè)的亮麗名片之一,某養(yǎng)殖場響應山東省加快新舊動能轉換的號召,今年采用新技術投資養(yǎng)殖了200萬籠扇貝,并且全部被訂購,已知每籠扇貝的成本是40元,售價是100元,打撈出售過程中發(fā)現(xiàn),一部分扇貝生長情況不合要求,最后只能按照25元一籠出售,如果純收入為![]() 萬元,不合要求的扇貝有
萬元,不合要求的扇貝有![]() 萬籠.
萬籠.
(1)求純收入![]() 關于
關于![]() 的關系式.
的關系式.
(2)當![]() 為何值時,養(yǎng)殖場不賠不嫌?
為何值時,養(yǎng)殖場不賠不嫌?
科目:初中數(shù)學 來源: 題型:
【題目】如圖,ABCD中,E,F(xiàn)是對角線BD上的兩點,如果添加一個條件,使△ABE≌△CDF,則添加的條件不能為( )

A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】下列說法正確的是( )
A. ![]() 一定是一次函數(shù)
一定是一次函數(shù)
B. 有的實數(shù)在數(shù)軸上找不到對應的點
C. 長為![]() 的三條線段能組成直角三角形
的三條線段能組成直角三角形
D. 無論![]() 為何值,點
為何值,點![]() 總是在第二象限
總是在第二象限
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】對于一次函數(shù)![]() ,下列結論錯誤的是( )
,下列結論錯誤的是( )
A.函數(shù)的圖象與![]() 軸的交點坐標是
軸的交點坐標是![]()
B.函數(shù)值隨自變量的增大而減小
C.函數(shù)的圖象不經(jīng)過第三象限
D.函數(shù)的圖象向下平移![]() 個單位長度得到
個單位長度得到![]() 的圖象
的圖象
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
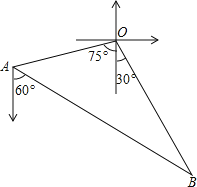
【題目】如圖,甲、乙兩漁船同時從港口O出發(fā)外出捕魚,乙沿南偏東![]() 方向以每小時15海里的速度航行,甲沿南偏西
方向以每小時15海里的速度航行,甲沿南偏西![]() 方向以每小時
方向以每小時![]() 海里的速度航行,當航行1小時后,甲在A處發(fā)現(xiàn)自己的漁具掉在乙船上,于是迅速改變航向和速度,仍以勻速沿南偏東
海里的速度航行,當航行1小時后,甲在A處發(fā)現(xiàn)自己的漁具掉在乙船上,于是迅速改變航向和速度,仍以勻速沿南偏東![]() 方向追趕乙船,正好在B處追上
方向追趕乙船,正好在B處追上![]() 甲船追趕乙船的速度為多少海里
甲船追趕乙船的速度為多少海里![]() 小時?
小時?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
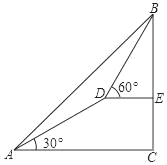
【題目】如圖,測量人員在山腳A處測得山頂B的仰角為45°,沿著仰角為30°的山坡前進1000米到達D處,在D處測得山頂B的仰角為60°,求山的高度?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】閱讀下列材料并完成任務:
中國古代三國時期吳國的數(shù)學家趙爽最早對勾股定理作出理論證明.他創(chuàng)制了一幅“勾股圓方圖”(如圖l),用數(shù)形結合的方法,給出了勾股定理的詳細證明.在這幅“勾股圓方圖”中,以弦為邊長得到的正方形![]() 是由
是由![]() 個全等的直角三角形再加上中間的那個小正方形組成的.每個直角三角形的面積為
個全等的直角三角形再加上中間的那個小正方形組成的.每個直角三角形的面積為![]() ;中間的小正方形邊長為
;中間的小正方形邊長為![]() ,面積為
,面積為![]() .于是便得到式子:
.于是便得到式子:![]() .趙爽的這個證明可謂別具匠心,極富創(chuàng)新意識.他用幾何圖形的截、割、拼、補來證明代數(shù)式之間的恒等關系,既具嚴密性,又具直觀性,為中國古代以形證數(shù)、形數(shù)統(tǒng)一、代數(shù)和幾何緊密結合、互不可分的獨特風格樹立了一個典范.如圖2,是“趙爽弦圖”,其中
.趙爽的這個證明可謂別具匠心,極富創(chuàng)新意識.他用幾何圖形的截、割、拼、補來證明代數(shù)式之間的恒等關系,既具嚴密性,又具直觀性,為中國古代以形證數(shù)、形數(shù)統(tǒng)一、代數(shù)和幾何緊密結合、互不可分的獨特風格樹立了一個典范.如圖2,是“趙爽弦圖”,其中![]() 、
、![]() 、
、![]() 和
和![]() 是四個全等的直角三角形,四邊形
是四個全等的直角三角形,四邊形![]() 和
和![]() 都是正方形,根據(jù)這個圖形的面積關系,可以證明勾股定理.設
都是正方形,根據(jù)這個圖形的面積關系,可以證明勾股定理.設![]() ,
,![]() ,
,![]() ,取
,取![]() ,
,![]() .
.
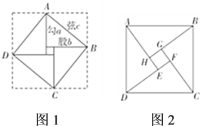
任務:
(1)填空:正方形![]() 的面積為______,四個直角三角形的面積和為______;
的面積為______,四個直角三角形的面積和為______;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在2016年“雙十一”期間,某快遞公司計劃租用甲、乙兩種車輛快遞貨物,從貨物量來計算:若租用兩種車輛合運,10天可以完成任務;若單獨租用乙種車輛,完成任務的天數(shù)是單獨租用甲種車輛完成任務天數(shù)的2倍.
(1)求甲、乙兩種車輛單獨完成任務分別需要多少天?
(2)已知租用甲、乙兩種車輛合運需租金65000元,甲種車輛每天的租金比乙種車輛每天的租金多1500元,試問:租甲和乙兩種車輛、單獨租甲種車輛、單獨租乙種車輛這三種租車方案中,哪一種租金最少?請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某單位要制作一批宣傳材料.甲公司提出:每份材料收費1元,另收取制版費600元;乙公司提出:每份材料收費1.2元,不收取制版費.
(1)設制作![]() 份宣傳材料,甲公司收費
份宣傳材料,甲公司收費![]() 元,乙公司收費
元,乙公司收費![]() 元,請分別寫出
元,請分別寫出![]() ,
,![]() 與
與![]() 的關系式;
的關系式;
(2)該單位要制作宣傳材料1000~4500(含1000和4500)份,選擇哪家公司比較合算?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com