
【題目】如圖,在△ABC中,∠BAC=90°,AD⊥BC于點D,BE交AD于點F,交AC于點E,若BE平分∠ABC,試判斷△AEF的形狀,并說明理由.

科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,![]() (1,5)、
(1,5)、![]() (1,0)、
(1,0)、![]() (4,3).
(4,3).

(1)在圖中作出△![]() 關于
關于![]() 軸的對稱圖形△
軸的對稱圖形△![]() ;
;
(2)寫出點![]() 、
、![]() 、
、![]() 的坐標;
的坐標;
(3)在![]() 軸上畫出點
軸上畫出點![]() ,使
,使![]() 最小;
最小;
(4)求六邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線![]() 與y軸交于點A.
與y軸交于點A.
(1)如圖,直線![]() 與直線
與直線![]() 交于點B,與y軸交于點C,點B橫坐標為
交于點B,與y軸交于點C,點B橫坐標為![]() .
.
①求點B的坐標及k的值;
②直線![]() 與直線
與直線![]() 與y軸所圍成的△ABC的面積等于 ;
與y軸所圍成的△ABC的面積等于 ;
(2)直線![]() 與x軸交于點E(
與x軸交于點E(![]() ,0),若
,0),若![]() ,求k的取值范圍.
,求k的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求證:AD平分∠BAC;
(2)直接寫出AB+AC與AE之間的等量關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P為∠AOB內一定點,M、N分別是射線OA、OB上一點,當△PMN周長最小時,∠OPM=50°,則∠AOB=( )
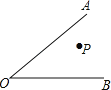
A.40°B.45°C.50°D.55°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于一元二次方程![]() ,下列說法:
,下列說法:
①若![]() ,方程
,方程![]() 有兩個不等的實數根;
有兩個不等的實數根;
②若方程![]() 有兩個不等的實數根,則方程
有兩個不等的實數根,則方程![]() 也一定有兩個不等的實數根;
也一定有兩個不等的實數根;
③若![]() 是方程
是方程![]() 的一個根,則一定有
的一個根,則一定有![]() 成立;
成立;
④若![]() 是方程
是方程![]() 的一個根,則一定有
的一個根,則一定有![]() 成立,其中正確的只有( )
成立,其中正確的只有( )
A. ①②④ B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目:初中數學 來源: 題型:
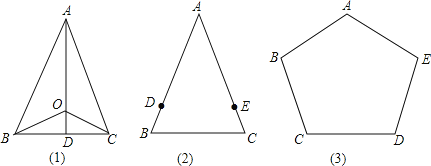
【題目】(1)如圖(1),在△ABC,AB=AC,O為△ABC內一點,且OB=OC,求證:直線AO垂直平分BC.以下是小明的證題思路,請補全框圖中的分析過程.

(2)如圖(2),在△ABC中,AB=AC,點D、E分別在AB、AC上,且BD=CE.請你只用無刻度的直尺畫出BC邊的垂直平分線(不寫畫法,保留畫圖痕跡).
(3)如圖(3),在五邊形ABCDE中,AB=AE,BC=DE,∠B=∠E,請你只用無刻度的直尺畫出CD邊的垂直平分線,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
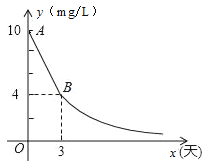
【題目】環保局對某企業排污情況進行檢測,結果顯示:所排污水中硫化物的濃度超標,即硫化物的濃度超過最高允許的1.0 mg/L.環保局要求該企業立即整改,在15天以內(含15天)排污達標.整改過程中,所排污水中硫化物的濃度y(mg/L)與時間x(天)的變化規律如圖所示,其中線段AB表示前3天的變化規律,其中第3天時硫化物的濃度降為4 mg/L.從第3天起所排污水中硫化物的濃度y與時間x滿足下面表格中的關系:
時間x(天) | 3 | 4 | 5 | 6 | 8 | …… |
硫化物的濃y(mg/L) | 4 | 3 | 2.4 | 2 | 1.5 |
(1)求整改過程中當0≤x<3時,硫化物的濃度y與時間x的函數表達式;
(2)求整改過程中當x≥3時,硫化物的濃度y與時間x的函數表達式;
(3)該企業所排污水中硫化物的濃度,能否在15天以內不超過最高允許的1.0 mg/L?為什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com