
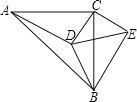
【題目】如圖:△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,連接BD,DE,BE,則下列結論:①∠ECA=165°,②BE=BC;③AD⊥BE;④![]() =1.其中正確的是( )
=1.其中正確的是( )
A.①②③
B.①②④
C.①③④
D.①②③④
【答案】D
【解析】
試題分析:①根據:∠CAD=30°,AC=BC=AD,利用等腰三角形的性質和三角形內角和定理即可求出∠ECA=165°,從而得證結論正確;
②根據CE⊥CD,∠ECA=165°,利用SAS求證△ACD≌△BCE即可得出結論;
③根據∠ACB=90°,∠CAD=30°,AC=BC,利用等腰三角形的性質和△ACD≌△BCE,求出∠CBE=30°,然后即可得出結論;
④過D作DM⊥AC于M,過D作DN⊥BC于N.由∠CAD=30°,可得CM=![]() AC,求證△CMD≌△CND,可得CN=DM=
AC,求證△CMD≌△CND,可得CN=DM=![]() AC=
AC=![]() BC,從而得出CN=BN.然后即可得出結論.
BC,從而得出CN=BN.然后即可得出結論.
解:①∵∠CAD=30°,AC=BC=AD,∴∠ACD=∠ADC=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∵CE⊥CD,∴∠DCE=90°,
∴∠ECA=165°∴①正確;
②∵CE⊥CD,∠ECA=165°(已證),
∴∠BCE=∠ECA﹣∠ACB=165﹣90=75°,
∴△ACD≌△BCE(SAS),
∴BE=BC,∴②正確;
③∵∠ACB=90°,∠CAD=30°,AC=BC,
∴∠CAB=∠ABC=45°
∴∠BAD=∠BAC﹣∠CAD=45﹣30=15°,
∵△ACD≌△BCE,
∴∠CBE=30°,
∴∠ABF=45+30=75°,
∴∠AFB=180﹣15﹣75=90°,
∴AD⊥BE.
④證明:如圖,
過D作DM⊥AC于M,過D作DN⊥BC于N.
∵∠CAD=30°,且DM=![]() AC,
AC,
∵AC=AD,∠CAD=30°,∴∠ACD=75°,
∴∠NCD=90°﹣∠ACD=15°,∠MDC=∠DMC﹣∠ACD=15°,
在△CMD和△CND中,
 ,
,
∴△CMD≌△CND,
∴CN=DM=![]() AC=
AC=![]() BC,
BC,
∴CN=BN.
∵DN⊥BC,
∴BD=CD.∴④正確.
所以4個結論都正確.
故選D.




 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】對于二次函數y = (x-1)2+2的圖像,下列說法正確的是( )
A. 開口向下; B. 頂點坐標(-1,2); C. 對稱軸是x =1; D. 與x軸有兩個交點
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某區新教師招聘中,七位評委獨立給出分數,得到一列數.若去掉一個最高分和一個最低分,得到一列新數,那么這兩列數的相關統計量中,一定相等的是 ( )
A. 中位數 B. 眾數 C. 方差 D. 平均數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E為AB的中點.
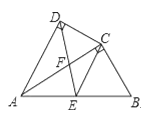
(1)求證:AC2=AB![]() AD;
AD;
(2)求證:CE∥AD;
(3)若AD=5,AB=7,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com