
【題目】如圖,在Rt△ABC中,∠ACB=90°,過點C的直線m∥AB,D為AB邊上一點,過點D作DE⊥BC,交直線m于點E,垂足為點F,連接CD,BE.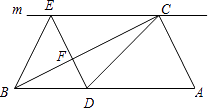
(1)求證:CE=AD;
(2)當點D是AB中點時,四邊形BECD是什么特殊四邊形?說明你的理由;
(3)當∠A的大小滿足什么條件時,四邊形BECD是正方形?(不需要證明)
【答案】
(1)
證明:∵直線m∥AB,
∴EC∥AD.
又∵∠ACB=90°,
∴BC⊥AC.
又∵DE⊥BC,
∴DE∥AC.
∵EC∥AD,DE∥AC,
∴四邊形ADEC是平行四邊形.
∴CE=AD
(2)
當點D是AB中點時,四邊形BECD是菱形.
證明:∵D是AB中點,DE∥AC(已證),
∴F為BC中點,
∴BF=CF
∵直線m∥AB,
∴∠ECF=∠DBF.
∵∠BFD=∠CFE,
∴△BFD≌△CFE
∴DF=EF.
∵DE⊥BC,
∴BC和DE垂直且互相平分.
∴四邊形BECD是菱形
(3)
當∠A的大小是45°時,四邊形BECD是正方形.
理由是:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D為BA中點,
∴CD⊥AB,
∴∠CDB=90°,
∵四邊形BECD是菱形,
∴四邊形BECD是正方形,
即當∠A=45°時,四邊形BECD是正方形
【解析】(1)由BC⊥AC,DE⊥BC,得到DE∥AC,從而判斷出四邊形ADEC是平行四邊形.即可,(2)先判斷出△BFD≌△CFE,再判斷出BC和DE垂直且互相平分,得到四邊形BECD是菱形.(3)先判斷出∠CDB=90°,從而得到有一個角是直角的菱形是正方形.
【考點精析】根據題目的已知條件,利用平行四邊形的判定的相關知識可以得到問題的答案,需要掌握兩組對邊分別平行的四邊形是平行四邊形:兩組對邊分別相等的四邊形是平行四邊形;一組對邊平行且相等的四邊形是平行四邊形;兩組對角分別相等的四邊形是平行四邊形;對角線互相平分的四邊形是平行四邊形.


科目:初中數學 來源: 題型:
【題目】小明某一天放學從學校回家,如圖,大致描述他回家過程中離家的距離S(千米)與所用時間t(分)之間的關系,下列說法錯誤的是( )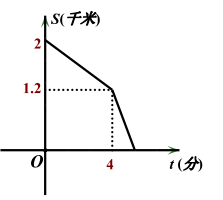
A.學校離家距離為2千米
B.前4分鐘,小明平均速度為200米/分鐘
C.騎了4分鐘后,小明加快了速度
D.騎了4分鐘時,小明離學校1.2千米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“賞中華詩詞,尋文化基因,品生活之美”,某校舉辦了首屆“中國詩詞大會”,經選拔后有50名學生參加決賽,這50名學生同時默寫50首古詩詞,若每正確默寫出一首古詩詞得2分,根據測試成績繪制出部分頻數分布表和部分頻數分布直方圖如圖表:

請結合圖表完成下列各題:
(1)①表中a的值為 ; ②頻數分布直方圖補充完整;
(2)若測試成績不低于80分為優秀,則本次測試的優秀率是
(3)第5組10名同學中,有4名男同學,現將這10名同學平均分成兩組進行對抗練習,且4名男同學每組分兩人,求小明與小強兩名男同學能分在同一組的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知F是以AC為直徑的半圓O上任意一點,過AC上任意一點H作AC的垂線分別交CF,AF的延長線于點E,B,點D是線段BE的中點.
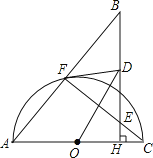
(1)求證:DF是⊙O的切線;
(2)若BF=AF,求證AF2=EF·CF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用配方法解方程x2﹣2x﹣1=0,原方程應變形為( )
A. (x﹣1)2=2 B. (x+1)2=2 C. (x﹣1)2=1 D. (x+1)2=1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在抗洪搶險中,解放軍戰士的沖鋒舟加滿油,沿東西方向的河流搶救災民,早晨從![]() 地出發,晚上到達
地出發,晚上到達![]() 地,約定向東為正方向,當天的航行路程記錄如下(單位:千米):
地,約定向東為正方向,當天的航行路程記錄如下(單位:千米): ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(![]() )請你幫忙確定
)請你幫忙確定![]() 地位于
地位于![]() 地的什么方向,距離
地的什么方向,距離![]() 地多少千米?
地多少千米?
(![]() )救災過程中,沖鋒舟離出發點
)救災過程中,沖鋒舟離出發點![]() 最遠處有多遠?(請直接寫出答案)
最遠處有多遠?(請直接寫出答案)
(![]() )若沖鋒舟每千米耗油
)若沖鋒舟每千米耗油![]() 升,油箱容量為
升,油箱容量為![]() 升,求沖鋒舟當天救災過程中至少還需補充多少升油?
升,求沖鋒舟當天救災過程中至少還需補充多少升油?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com