
【題目】如圖,G是正方形形ABCD的邊BC上一點,DE、BF分別垂直AG于點E、F,則圖中與△ABF相似的三角形有( )
A.1個
B.2個
C.3個
D.4個
【答案】C
【解析】解:∵BF⊥AG,
∴∠AFB=∠BFG=∠ABG=90°.
∵∠BAF+∠ABF=90°,∠ABF+∠FBG=90°,
∴∠BAF=∠GBF,
∴△ABF∽△BGF;
同理可得,△ABF∽△AGB,△ABF∽△DAE.
所以答案是:C.
【考點精析】解答此題的關鍵在于理解余角和補角的特征的相關知識,掌握互余、互補是指兩個角的數量關系,與兩個角的位置無關,以及對正方形的性質的理解,了解正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形.


科目:初中數學 來源: 題型:
【題目】填空,將理由補充完整.
如圖,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() ,求證:
,求證:![]() .
.

證明:∵![]() ,
,![]() (已知)
(已知)
∴![]() (垂直的定義)
(垂直的定義)
∴![]() (________________________)
(________________________)
∴![]() (________________________)
(________________________)
∵![]() (已知)
(已知)
又∵![]() (________________________)
(________________________)
∴![]() (________________________)
(________________________)
∴![]() (________________________)
(________________________)
∴![]() (________________________)
(________________________)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠1=∠3,CD∥EF,試說明∠1=∠4.請將過程填寫完整.

解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(兩直線平行,同位角相等).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,點P在線段AB外,且PA=PB,求證:點P在線段AB的垂直平分線上,在證明該結論時,需添加輔助線,則作法不正確的是( )

A. 作∠APB的平分線PC交AB于點C
B. 過點P作PC⊥AB于點C且AC=BC
C. 取AB中點C,連接PC
D. 過點P作PC⊥AB,垂足為C
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知等腰三角形ABC中,AB=AC,點D、E分別在邊AB、AC上,且AD=AE,連接BE、CD,交于點F.
(1)判斷∠ABE與∠ACD的數量關系,并說明理由;
(2)求證:過點A、F的直線垂直平分線段BC.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() ,點
,點![]() 是
是![]() 軸上兩點,其中
軸上兩點,其中![]() ,點
,點![]() 都在
都在![]() 軸上,
軸上,![]() 在射線
在射線![]() 上(不與點
上(不與點![]() 重合),
重合),![]() ,連結
,連結![]() .
.
(1)求![]() 、
、![]() 的坐標;
的坐標;
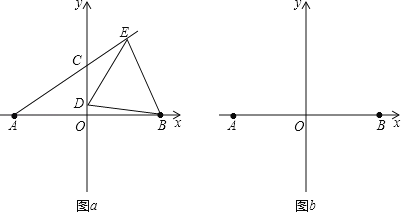
(2)如圖![]() ,若
,若![]() 在
在![]() 軸正半軸,
軸正半軸,![]() 在線段
在線段![]() 上,當
上,當![]() 時,求證:
時,求證:![]() 為等邊三角形;(提示:連結
為等邊三角形;(提示:連結![]() )
)
(3)當![]() 時,在圖
時,在圖![]() 中畫出示意圖,設
中畫出示意圖,設![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com