
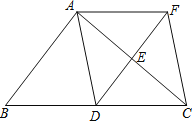
【題目】如圖,在△ABC中,點(diǎn)D、E分別是邊BC、AC的中點(diǎn),過點(diǎn)A作AF∥BC交DE的延長線于F點(diǎn),連接AD、CF.
(1)求證:四邊形ADCF是平行四邊形;
(2)當(dāng)△ABC滿足什么條件時,四邊形ADCF是正方形?請說明理由.
【答案】(1)證明見解析;(2)等腰直角三角形.
【解析】試題分析:
(1)先證四邊形ABDF是平行四邊形,再證結(jié)論;
(2)由四邊形ADCF是正方形來證明△ABC是等腰直角三角形.
試題解析:
(1)證明:∵點(diǎn)D、E分別是邊BC、AC的中點(diǎn),∴DE∥AB,
∵AF∥BC,∴四邊形ABDF是平行四邊形,∴AF=BD,則AF=DC=AD,
∵AF∥BC,∴四邊形ADCF是平行四邊形;
(2)當(dāng)△ABC是等腰直角三角形時,四邊形ADCF是正方形,
理由:∵四邊形ADCF是正方形,∴∠ADC=90°,AC=DF,AF=DC.
∵點(diǎn)D,E分別是邊BC,AC的中點(diǎn),AB=2DE,∴AB=DF,所以AB=AC.
∴四邊形ABDF是平行四邊形,∴AF=BD,∴BD=CD=AD,
∴∠BAC=90°,
∴△ABC是等腰直角三角形.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
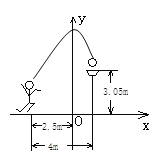
【題目】如圖所示,一位籃球運(yùn)動員在離籃圈水平距離為4m處跳起投籃,球沿一條拋物線運(yùn)行,當(dāng)球運(yùn)行的水平距離為2.5m時,達(dá)到最大高度3.5m,然后準(zhǔn)確落入籃框內(nèi).已知籃圈中心離地面距離為3.05m.
(1)建立如圖所示的直角坐標(biāo)系,求拋物線所對應(yīng)的函數(shù)關(guān)系式;
(2)若該運(yùn)動員身高1.8m,這次跳投時,球在他頭頂上方0.25m處出手.問:球出手時,他跳離地面多高?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 中,
中, ![]() ,
, ![]() .如圖,將
.如圖,將![]() 進(jìn)行折疊,使點(diǎn)
進(jìn)行折疊,使點(diǎn)![]() 落在線段
落在線段![]() 上(包括點(diǎn)
上(包括點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() ),設(shè)點(diǎn)
),設(shè)點(diǎn)![]() 的落點(diǎn)為
的落點(diǎn)為![]() ,折痕為
,折痕為![]() ,當(dāng)
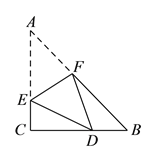
,當(dāng)![]() 是等腰三角形時,點(diǎn)
是等腰三角形時,點(diǎn)![]() 可能的位置共有( ).
可能的位置共有( ).
A. ![]() 種 B.
種 B. ![]() 種 C.
種 C. ![]() 種 D.
種 D. ![]() 種
種
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖:已知在△ABC中,AB=AC,D為BC邊的中點(diǎn),過點(diǎn)D作DE⊥AB,DF⊥AC,,垂足分別為E,F.
(1)求證:△BED≌△CFD;
(2)若∠A=90°,求證:四邊形DFAE是正方形.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
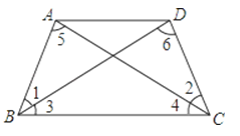
【題目】如圖,已知∠3=∠4,要說明△ABC≌△DCB,
(1)若以“SAS”為依據(jù),則需添加一個條件是________
(2)若以“AAS”為依據(jù),則需添加一個條件是________
(3)若以“ASA”為依據(jù),則需添加一個條件是________
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
(![]() )在
)在![]() 軸上是否存在點(diǎn)
軸上是否存在點(diǎn)![]() ,使
,使![]() 為等腰三角形,求出點(diǎn)
為等腰三角形,求出點(diǎn)![]() 坐標(biāo).
坐標(biāo).
(![]() )在
)在![]() 軸上方存在點(diǎn)
軸上方存在點(diǎn)![]() ,使以點(diǎn)
,使以點(diǎn)![]() ,
, ![]() ,
, ![]() 為頂點(diǎn)的三角形與
為頂點(diǎn)的三角形與![]() 全等,畫出
全等,畫出![]() 并請直接寫出點(diǎn)
并請直接寫出點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
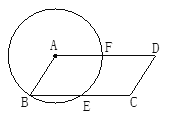
【題目】如圖,以![]() ABCD的頂點(diǎn)A為圓心,AB為半徑作圓,分別交BC、AD于E、F,若∠D=50°,求
ABCD的頂點(diǎn)A為圓心,AB為半徑作圓,分別交BC、AD于E、F,若∠D=50°,求![]() 的度數(shù)和
的度數(shù)和![]() 的度數(shù).
的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】一個不透明的袋子中裝有紅、白兩種顏色的小球,這些球除顏色外都相同,其中紅球有1個,若從中隨機(jī)摸出一個球,這個球是白球的概率為![]() .
.
(1)求袋子中白球的個數(shù);(請通過列式或列方程解答)
(2)隨機(jī)摸出一個球后,放回并攪勻,再隨機(jī)摸出一個球,求兩次都摸到相同顏色的小球的概率.(請結(jié)合樹狀圖或列表解答)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com