
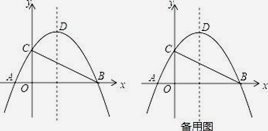
【題目】如圖,在平面直角坐標系中,拋物線y=ax2﹣3ax﹣4a的圖象經過點C(0,2),交x軸于點A、B(A點在B點左側),頂點為D.
(1)求拋物線的解析式及點A、B的坐標;
(2)將△ABC沿直線BC對折,點A的對稱點為A′,試求A′的坐標;
(3)拋物線的對稱軸上是否存在點P,使∠BPC=∠BAC?若存在,求出點P的坐標;若不存在,請說明理由.
【答案】(1)A(﹣1,0),B(4,0).(2)A'(1,4);(3)P的坐標為(![]() ,-
,-![]() )或(
)或(![]() ,2+
,2+![]() ).
).
【解析】試題分析:(1)將(0,2)代入拋物線解析式求得a的值,從而得出拋物線的解析式,再令y=0,得出x的值,即可求得點A、B的坐標;
(2)如圖2,作A'H⊥x軸于H,可證明△AOC∽△COB,得出∠ACO=∠CBO,由A'H∥OC,即可得出A′H的長,即可求得A′的坐標;
(3)分兩種情況:①如圖3,以AB為直徑作⊙M,⊙M交拋物線的對稱軸于P(BC的下方),由圓周角定理得出點P坐標;②如圖4,類比第(2)小題的背景將△ABC沿直線BC對折,點A的對稱點為A',以A'B為直徑作⊙M',⊙M'交拋物線的對稱軸于P'(BC的上方),作M'E⊥A'H于E,交對稱軸于F,求得M'F,在Rt△M'P'F中,由勾股定理得出P'F得的長,從而得出點P的坐標即可.
解:(1)把C(0,2)代入y=ax2﹣3ax﹣4a得﹣4a=2,
解得![]() .
.
所以拋物線的解析式為![]() .
.
令![]() ,可得:x1=﹣1,x2=4.
,可得:x1=﹣1,x2=4.
所以A(﹣1,0),B(4,0).
(2)如圖2,作A'H⊥x軸于H,
因為![]() ,且∠AOC=∠COB=90°,
,且∠AOC=∠COB=90°,
所以△AOC∽△COB,
所以∠ACO=∠CBO,可得∠ACB=∠OBC+∠BCO=90°,
由A'H∥OC,AC=A'C得OH=OA=1,A'H=2OC=4;
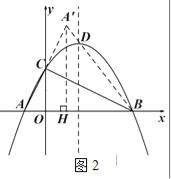
所以A'(1,4);
(3)分兩種情況:
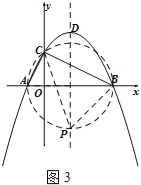
①如圖3,以AB為直徑作⊙M,⊙M交拋物線的對稱軸于P(BC的下方),
由圓周角定理得∠CPB=∠CAB,
易得:MP=![]() AB.所以P(
AB.所以P(![]() ,
,![]() ).
).
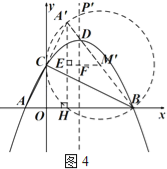
②如圖4,類比第(2)小題的背景將△ABC沿直線BC對折,
點A的對稱點為A',以A'B為直徑作⊙M',⊙M'交拋物線的對稱軸于P'(BC的上方),
則∠CP2B=∠CA'B=∠CAB.
作M'E⊥A'H于E,交對稱軸于F.
則M'E=![]() BH=
BH=![]() ,EF=
,EF=![]() =
=![]() .
.
所以M'F=![]() =1.
=1.
在Rt△M'P'F中,P'F=![]() ,
,
所以P'M=2+![]() .
.
所以P'(![]() ,2+
,2+![]() ).
).
綜上所述,P的坐標為(![]() ,
,![]() )或(
)或(![]() ,2+
,2+![]() ).
).


科目:初中數學 來源: 題型:
【題目】你吃過拉面嗎?實際上在做拉面的過程中就滲透著數學知識:一定體積的面團做成拉面,面條的總長度y(m)是面條的粗細(橫截面積)s(mm2)的反比例函數,其圖象如圖.
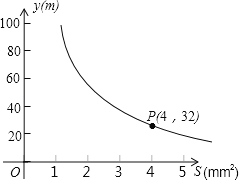
(1)寫出y與s的函數關系式;
(2)求當面條粗3.2mm2時,面條的總長度是多少m?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“喜愛哪種動物的同學最多”的調查活動中,調查了全班60名同學,其中喜歡大熊貓的同學占70%,則喜歡大熊貓的學生人數是( ).
A. 42 B. 45 C. 60 D. 75
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程mx2﹣(m+2)x+2=0
(1)若方程的一個根為3,求m的值及另一個根;
(2)若該方程根的判別式的值等于1,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對平面上任意一點(a,b),定義f,g兩種變換:f(a,b)=(a,﹣b)如:f(1,2)=(1,﹣2);g(a,b)=(b,a).如:g(1,2)=(2,1).據此得g(f(5,﹣9))=________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com