
【題目】在一次中學生田徑運動會上,根據參加男子跳高初賽的運動員的成績(單位:m),繪制出如下兩幅統計圖.請根據相關信息,解答下列問題:
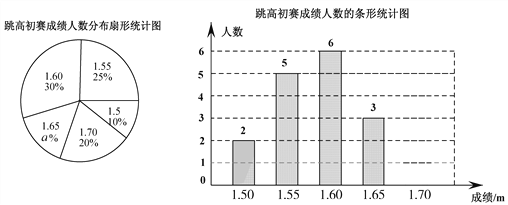
(1)扇形統計圖中,初賽成績為1.65m所在扇形圖形的圓心角為_ _°;
(2)補全條形統計圖;
(3)這組初賽成績的中位數是 m;
(4)根據這組初賽成績確定8人進入復賽,那么初賽成績為1.60m的運動員楊強能否進入復賽?為什么?
【答案】(1)54°;
(2)補全圖形見解析;
(3)1.60;
(4)不一定,理由見解析.
【解析】試題分析:(1)用整體1減去其它所占的百分比,即可求出a的值;用360°乘以初賽成績為1.70m所占的百分比即可;
(2)根據跳1.50m的人數和所占的百分比求出總人數,再乘以跳170m的人數所占的百分比,求出跳170m的人數,從而補全統計圖;
(3)根據眾數和中位數的定義分別進行解答即可;
(4)根據中位數的意義可直接判斷出能否進入復賽.
試題解析:(1)根據題意得:
1-20%-10%-25%-30%=15%;
則a的值是15;
初賽成績為1.70m所在扇形圖形的圓心角為:360°×20%=72°;
(2)跳170m的人數是: ![]() ×20%=4(人),
×20%=4(人),
補圖如下: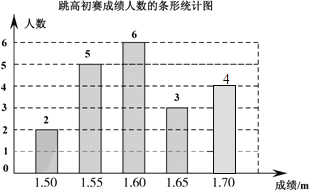
(3)∵在這組數據中,1.60m出現了6次,出現的次數最多,
∴這組數據的眾數是1.60m;
將這組數據從小到大排列,其中處于中間的兩個數都是1.60m,
則這組數據的中位數是1.60m.
(4)不一定,理由如下:
因為由高到低的初賽成績中有4人是1.70m,有3人是1.65m,第8人的成績為1.60m,但是成績為1.60m的有6人,所以楊強不一定進入復賽.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:初中數學 來源: 題型:
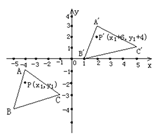
【題目】如圖所示,△A′B′C′是△ABC經過平移得到的,△ABC中任意一點P(x1,y1)平移后的對應點為P′(x1+6,y1+4)。
(1)請寫出三角形ABC平移的過程;
(2)分別寫出點A′,B′,C′ 的坐標。
(3)求△A′B′C′的面積。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直角坐標系內有四個點A(-1,2),B(3,0),C(1,4),D(x,y),若以A,B,C,D為頂點的四邊形是平行四邊形,則D點的坐標為___________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:△ABC中,AB=AC,∠B=α.
(1)如圖1,點D,E分別在邊AB,AC上,線段DE的垂直平分線MN交直線BC于點M,交DE于點N,求證:BD+CE=BC.需補充條件∠EMN= (用含α的式子表示)補充條件后并證明;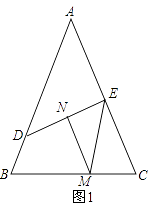
(2)把(1)中的條件改為點D,E分別在邊BA、AC延長線上,線段DE的垂直平分線MN交直線BC于點M,交DE于點N(如圖2),并補充條件∠EMN=(用含α的式子表示),通過觀察或測量,猜想線段BD,CE與BC之間滿足的數量關系,并予以證明.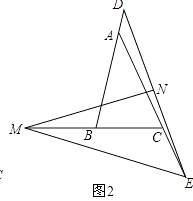
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的口袋裝有若干個紅、黃、藍、綠四種顏色的小球,小球除顏色外完全相同,為估計該口袋中四種顏色的小球數量,每次從口袋中隨機摸出一球記下顏色并放回,重復多次試驗,匯總實驗結果繪制如圖不完整的條形統計圖和扇形統計圖.
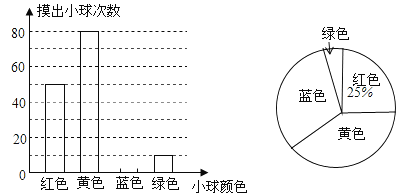
根據以上信息解答下列問題:
(1)求實驗總次數,并補全條形統計圖;
(2)扇形統計圖中,摸到黃色小球次數所在扇形的圓心角度數為多少度?
(3)已知該口袋中有10個紅球,請你根據實驗結果估計口袋中綠球的數量.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com