
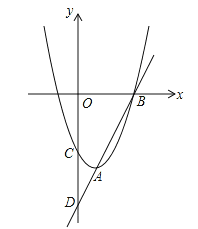
【題目】如圖,已知直線y=kx-6與拋物線y=ax2+bx+c相交于A,B兩點,且點
A(1,-4)為拋物線的頂點,點B在x軸上.直線AB交y軸于點D,拋物線交y軸于點C.
(1)求直線AB的解析式;
(2)求拋物線的解析式;
(3)在y軸上是否存在點Q,使△ABQ為直角三角形?若存在,請求出點Q的坐標;若不存在,請說明理由。
【答案】(1)y=2x-6,(2)y=x2-2x-3;(3)(0,-![]() )或(0,
)或(0,![]() )或(0,-1)或(0,-3).
)或(0,-1)或(0,-3).
【解析】
試題分析:(1)把點A坐標代入y=kx-6,根據待定系數法即可求得直線AB的解析式;
(2)根據直線AB的解析式求出點B的坐標,點A是拋物線的頂點,那么可以將拋物線的解析式設為頂點式,再代入點B的坐標,依據待定系數法即可求解;
(3)分別以A、B、Q為直角頂點,分類進行討論.找出相關的相似三角形,依據對應線段成比例進行求解即可.
試題解析:(1)把A(1,-4)代入y=kx-6,得k=2,
∴直線AB的解析式為y=2x-6,
(2)∵拋物線的頂點為A(1,-4),
∴設此拋物線的解析式為y=a(x-1)2-4,
∵點B在直線y=2x-6上,且橫坐標為0,
∴點B的坐標為(3,0),
又∵點B在拋物線y=a(x-1)2-4上,
∴a(3-1)2-4=0,解之得a=1,
∴此拋物線的解析式為y=(x-1)2-4,即y=x2-2x-3;
(3)在y軸上存在點Q,使△ABQ為直角三角形.理由如下:
作AE⊥y軸,垂足為點E.
又∵點D是直線y=2x-6與y軸的交點,點C是拋物線y=x2-2x-3與y軸的交點
∴E(0,-4),D(0,-6),C(0,-3)
∴OD=6,OE=4,AE=1,ED=2,OC=3,OB=3,BD=![]() ,AD=
,AD=![]()
①如圖,當∠Q1AB=90°時,△DAQ1∽△DOB,
∴![]() ,即
,即![]() ,
,
∴DQ1=![]() ,
,
∴OQ1=6-![]() =
=![]() ,即Q1(0,-
,即Q1(0,-![]() );
);
②如圖,當∠Q2BA=90°時,△BOQ2∽△DOB,
∴![]() ,即
,即![]() ,
,
∴OQ2=![]() ,即Q2(0,
,即Q2(0,![]() );
);
③如圖,當∠AQ3B=90°時,則△BOQ3∽△Q3EA,
∴![]() ,即
,即![]() ,
,
∴OQ32-4OQ3+3=0,
∴OQ3=1或3,
即Q3(0,-1),Q4(0,-3).
綜上,Q點坐標為(0,-![]() )或(0,
)或(0,![]() )或(0,-1)或(0,-3).
)或(0,-1)或(0,-3).



科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=20cm,BC=16cm,點D為線段AB的中點,動點P以2cm/s的速度從B點出發在射線BC上運動,同時點Q以a cm/s(a>0且a≠2)的速度從C點出發在線段CA上運動,設運動時間為x秒.
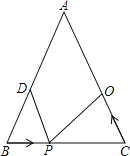
(1)若AB=AC,P在線段BC上,求當a為何值時,能夠使△BPD和△CQP全等?
(2)若∠B=60°,求出發幾秒后,△BDP為直角三角形?
(3)若∠C=70°,當∠CPQ的度數為多少時,△CPQ為等腰三角形?(請直接寫出答案,不必寫出過程).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某旅游景點門票價格規定如下:

某校七年級組織甲、乙兩個班共92人去該景點游玩,其中甲班人數多余乙班人數且甲班人數不夠90人,如果兩個班單獨購買門票,一共應付7760元.
(1)如果甲、乙兩個班聯合起來購買門票,那么比各自購買門票可以節省多少錢?
(2)甲、乙兩個班各有多少學生?
(3)如果甲班有10名學生因學校有任務不能參加這次旅游,請你作為兩個班設計出購買門票的方案,并指出最省錢的方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校初中三年級270名師生計劃集體外出一日游,乘車往返,經與客運公司聯系,他們有座位數不同的中巴車和大客車兩種車型可供選擇,每輛大客車比中巴車多15個座位,學校根據中巴車和大客車的座位數計算后得知,如果租用中巴車若干輛,師生剛好坐滿全部座位;如果租用大客車,不僅少用一輛,而且師生坐完后還多30個座位.
(1)求中巴車和大客車各有多少個座位?
(2)客運公司為學校這次活動提供的報價是:租用中巴車每輛往返費用350元,租用大客車每輛往返費用400元,學校在研究租車方案時發現,同時租用兩種車,其中大客車比中巴車多租一輛,所需租車費比單獨租用一種車型都要便宜,按這種方案需要中巴車和大客車各多少輛?租車費比單獨租用中巴車或大客車各少多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線C1是二次函數y=x2﹣10x在第四象限的一段圖象,它與x軸的交點是O、A1;將C1繞點A1旋轉180°后得拋物線C2;交x軸于點A2;再將拋物線C2繞A2點旋轉180°后得拋物線C3,交x軸于點A3;如此反復進行下去…
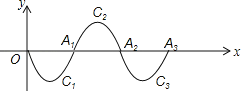
(1)拋物線C3與x軸的交點A3的坐標是多少?拋物線Cn與x軸的交點An的坐標是多少?
(2)若某段拋物線上有一點P(2016,a),試求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知E、F分別是ABCD的邊BC、AD上的點,且BE=DF.

(1)求證:四邊形AECF是平行四邊形;
(2)若∠BAC=90°,AC平分∠EAF,且BC=8cm,求BE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com