【題目】根據下列已知條件，能畫出唯一的△ABC的是( )
A. AB＝3，BC＝4，CA＝8 B. AB＝4，BC＝3，∠A＝30°
C. ∠A＝35°，∠B＝65°，AB＝7 D. ∠C＝90°，AB＝8
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】將△ABC繞點A按逆時針方向旋轉θ度，并使各邊長變為原來的n倍，得△AB′C′ ，如圖①所示，∠BAB′ ＝θ， 
，我們將這種變換記為[θ，n] ．
（1）如圖①，對△ABC作變換[60°，
]得到△AB′C′ ，則
:
= ；直線BC與直線B′C′所夾的銳角為 度；
（2）如圖②，△ABC中，∠BAC=30°，∠ACB=90°，對△ABC作變換[θ，n]得到△AB′C′，使點B、C、
在同一直線上，且四邊形ABB′C′為矩形，求θ和n的值；
（3）如圖③，△ABC中，AB=AC，∠BAC=36°，BC=1，對△ABC作變換[θ，n]得到△AB′C′，使點B、C、B′在同一直線上，且四邊形ABB′C′為平行四邊形，求θ和n的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某賓館重新裝修后，準備在大廳的主樓梯上鋪設某種紅地毯，已知這種地毯售價為30元/m2 ， 主樓梯寬2m，其側面如圖所示．
（1）求這個地毯的長是多少？
（2）求這個地毯的面積是多少平方米？
（3）求購買地毯至少需要多少元錢？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，長方形ABCD在坐標平面內，點A的坐標是A（2，1），且邊AB、CD與x軸平行，邊AD、BC與x軸平行，點B、C的坐標分別為B（a，1），C（a，c），且a、c滿足關系式．c=
+
+3
（1）求B、C、D三點的坐標；
（2）怎樣平移，才能使A點與原點重合？平移后點B、C、D的對應分別為B1C1D1 ， 求四邊形OB1C1D1的面積；
（3）平移后在x軸上是否存在點P，連接PD，使S△COP=S四邊形OBCD？若存在這樣的點P，求出點P的坐標；若不存在，試說明理由．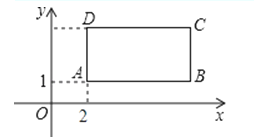
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（本題滿分10分）如圖，在平行四邊形ABCD中，點A、B、C的坐標分別是（1，0）、（3，1）、（3，3），雙曲線y=
（k≠0，x＞0）過點D．
（1）求此雙曲線的解析式；
（2）作直線AC交y軸于點E，連結DE，求△ CDE的面積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
