
【題目】太原市公共自行車的建設速度、單日租騎量等四項指標穩居全國首位.公共自行車車樁的截面示意圖如圖所示,AB⊥AD,AD⊥DC,點B,C在EF上,EF∥HG,EH⊥HG,AB=75cm,AD=24cm,BC=25cm,EH=4cm,則點A到地面的距離是 cm.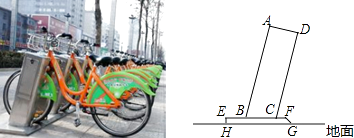
【答案】76
【解析】解:過點A作AM⊥BF于點M,過點C作CN⊥AB于點N,如圖所示:
∵AD=24cm,則NC=24cm,
∴BN= ![]() =
= ![]() =7(cm),
=7(cm),
∵∠AMB=∠CNB=90°,∠ABM=∠CBN,
∴△BNC∽△BMA,
∴ ![]() ,
,
∴ ![]() ,
,
解得:AM=72,
故點A到地面的距離=72+4=76(cm).
所以答案是:76.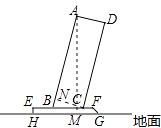
【考點精析】關于本題考查的相似三角形的性質和相似三角形的應用,需要了解對應角相等,對應邊成比例的兩個三角形叫做相似三角形;測高:測量不能到達頂部的物體的高度,通常用“在同一時刻物高與影長成比例”的原理解決;測距:測量不能到達兩點間的舉例,常構造相似三角形求解才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】如圖,直線PM切⊙O于點M,直線PO交⊙O于A、B兩點,弦AC∥PM,連接OM、BC.求證: 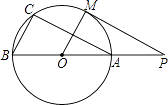
(1)△ABC∽△POM;
(2)2OA2=OPBC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程k2x2﹣2(k+1)x+1=0有兩個實數根.
(1)求k的取值范圍;
(2)當k=1時,設所給方程的兩個根分別為x1和x2 , 求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將長方形ABCD沿著對角線BD折疊,使點C落在![]() 處,
處,![]() 交AD于點E.
交AD于點E.
(1)試判斷△BDE的形狀,并說明理由;
(2)若![]() ,
,![]() ,求△BDE的面積.
,求△BDE的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某醫藥研究所開發了一種新藥,在試驗藥效時發現,如果成人按規定劑量服用,那么服藥后2小時時血液中含藥量最高,達每毫升8微克(1000微克=1毫克),接著逐步衰減,10小時時血液中含藥量為每毫升4微克,每毫升血液中含藥量y(微克),隨時間x(小時)的變化如圖所示.當成人按規定劑量服藥后:
(1)求y與x之間的解析式;
(2)如果每毫升血液中含藥量不低于3微克或3微克以上時,在治療疾病時是有效的,那么這個有效時間是多少小時?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知:在平面直角坐標系中,每個小正方形的邊長為1,△ABC的頂點都在格點上,點A的坐標為(-3,2).請按要求分別完成下列各小題:
(1)把△ABC向下平移7個單位,再向右平移7個單位,得到△A1B1C1,畫出△A1B1C1;
(2)畫出△A1B1C1關于x軸對稱的△A2B2C2;
畫出△A1B1C1關于y軸對稱的△A3B3C3;
(3)求△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】感知:如圖①,點E在正方形ABCD的BC邊上,BF⊥AE于點F,DG⊥AE于點G.可知△ADG≌△BAF.(不要求證明)

拓展:如圖②,點B、C在∠MAN的邊AM、AN上,點E, F在∠MAN內部的射線AD上,∠1、∠2分別是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求證:△ABE≌△CAF.
應用:如圖③,在等腰三角形ABC中,AB=AC,AB>BC.點D在邊B上.CD=2BD.點E, F在線段AD上.∠1=∠2=∠BAC.若△ABC的面積為9,則△ABE與△CDF的面積之和為_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某大學畢業生響應國家“自主創業”的號召,投資開辦了一個裝飾品商店,該店購進一種新上市的飾品進行了30天的試銷售,購進價格為40元/件.銷售結束后,得知日銷售量P(件)與銷售時間x(天)之間有如下關系:P=﹣2x+120(1≤x≤30,且x為整數);銷售價格Q(元/件)與銷售時間x(天)之間有如下關系:Q= ![]() x+50(1≤x≤30,且x為整數).
x+50(1≤x≤30,且x為整數).
(1)試求出該商店日銷售利潤w(元)與銷售時間x(天)之間的函數關系式;
(2)在這30天的試銷售中,哪一天的日銷售利潤最大,哪一天的日銷售利潤最小?并分別求出這個最大利潤和最小利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知⊙O是以AB為直徑的△ABC的外接圓,OD∥BC,交⊙O于點D,交AC于點E,連接BD,BD交AC于點F,延長AC到點P,連接PB. 
(1)若PF=PB,求證:PB是⊙O的切線;
(2)如果AB=10,BC=6,求CE的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com