
【題目】已知:△ABC 內接于⊙O,過點 A 作⊙O 的切線交 CB 的延長線于點 P,且∠PAB=45°.
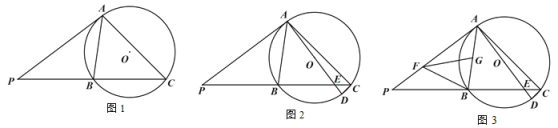
(1)如圖 1,求∠ACB 的度數;
(2)如圖 2,AD 是⊙O 的直徑,AD 交 BC 于點 E,連接 CD,求證:AC CD ![]() ;
;
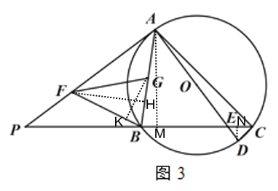
(3)如圖 3 ,在(2)的條件下,當 BC 4![]() CD 時,點 F,G 分別在 AP,AB 上,連接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的長.
CD 時,點 F,G 分別在 AP,AB 上,連接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的長.
【答案】(1)∠ACB=45°;(2)見解析;(3)![]()
【解析】
(1)連接OA,OB,根據切線的性質求出∠OAB=∠OBA=45°,得到∠AOB=90°,再根據圓周角定理可得答案;
(2)作AM⊥BC于M,DN⊥BC于N,連接BD,易求![]() ,
,![]() ,然后證明△ABM≌△BDN,得到AM=BN,等量代換即可得證;
,然后證明△ABM≌△BDN,得到AM=BN,等量代換即可得證;
(3)根據(2)中結論求出![]() ,然后證明△AMC∽△DNC,AM∥DN,根據相似三角形的性質和平行線分線段成比例定理求得DE和AD,進而利用勾股定理求出CD,AC,然后即可求出AB的長,再證明△PAB∽△PCA,求出PA,可得
,然后證明△AMC∽△DNC,AM∥DN,根據相似三角形的性質和平行線分線段成比例定理求得DE和AD,進而利用勾股定理求出CD,AC,然后即可求出AB的長,再證明△PAB∽△PCA,求出PA,可得![]() ,過點G作GK⊥FB,過點F作FH⊥BG,設GK=3b,利用三角函數及等腰三角形的性質求出AH和BH,然后列方程求出b值即可解決問題.
,過點G作GK⊥FB,過點F作FH⊥BG,設GK=3b,利用三角函數及等腰三角形的性質求出AH和BH,然后列方程求出b值即可解決問題.
解:(1)連接OA,OB,則OA=OB,
∴∠OAB=∠OBA,
∵PA是⊙O的切線,
∴∠PAO=90°,
∵∠PAB=45°,
∴∠OAB=∠OBA=45°,
∴∠AOB=90°,
∴∠ACB=![]() ∠AOB=45°;
∠AOB=45°;
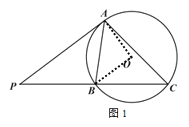
(2)作AM⊥BC于M,DN⊥BC于N,連接BD,
∵AD是⊙O的直徑,
∴∠ABD=∠ACD=90°,
∵∠ACB=45°,
∴∠CAM=∠BCD=∠CDN=45°,
∴![]() ,
,![]() ,
,
∵∠ADB=∠ACB=45°,
∴AB=BD,
∵∠ABM+∠DBN=90°=∠BDN+∠DBN,
∴∠ABM=∠BDN,
又∵∠AMB=∠BND=90°,
∴△ABM≌△BDN(AAS),
∴AM=BN,
∴![]() ;
;
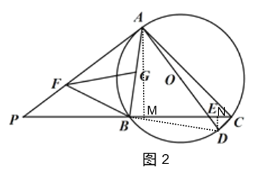
(3)如圖3,作AM⊥BC于M,DN⊥BC于N,由(2)可知:![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
設CD=x,則AC=7x,
∵∠AMC=∠DNC=90°,∠ACM=∠DCN=45°,
∴△AMC∽△DNC,
∴![]() ,
,
∵AM⊥BC,DN⊥BC,
∴AM∥DN,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
在Rt△ACD中,AC2+CD2=AD2,
∴![]() ,
,
解得:![]() (負值已舍去),
(負值已舍去),
∴![]() ,
,![]() ,
,![]() ,
,
∵△AMC是等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∴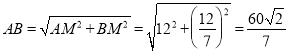 ,
,
∵∠P=∠P,∠PAB=∠PCA=45°,
∴△PAB∽△PCA,
∴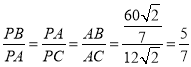 ,
,
設PB=5a,則PA=7a,
由PA2=PB·PC得:![]() ,
,
解得:![]() 或a=0(舍去),
或a=0(舍去),
∴PA=20,
∴![]() ,
,
∴![]() ,
,
過點G作GK⊥FB,過點F作FH⊥BG,
設GK=3b,則BF=FG=5b,
∴FK=4b,
∴BK=b,
∴![]() ,
,
∴BH![]() ,
,
∴ ,
,
∵∠PAB=45°,
∴AH=FH=![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
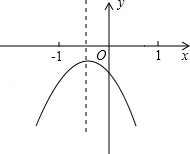
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,在下列五個結論中:
①2a﹣b<0;②abc<0;③a+b+c<0;④a﹣b+c>0;⑤4a+2b+c>0,
錯誤的個數有( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新型冠狀病毒肺炎是一種急性感染性肺炎,其病原體是一種先前未在人體中發現的新型冠狀病毒.市民出于防疫的需求,持續搶購防護用品.某藥店口罩每袋售價20元,醫用酒精每瓶售價15元.
(1)該藥店第一周口罩的銷售袋數比醫用酒精的銷售瓶數多100,且第一周這兩種防護用品的總銷售額為9000元,求該藥店第一周銷售口罩多少袋?
(2)由于疫情緊張,該藥店為了幫助大家共渡難關,第二周口罩售價降低了![]() ,銷量比第一周增加了
,銷量比第一周增加了![]() ,醫用酒精的售價保持不變,銷量比第一周增加了
,醫用酒精的售價保持不變,銷量比第一周增加了![]() ,結果口罩和醫用酒精第二周的總銷售額比第一周增加了
,結果口罩和醫用酒精第二周的總銷售額比第一周增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在甲、乙兩個不透明的布袋里,都裝有3個大小、材質完全相同的小球,其中甲袋中的小球上分別標有數字0,1,2;乙袋中的小球上分別標有數字﹣1,﹣2,0.現從甲袋中任意摸出一個小球,記其標有的數字為x,再從乙袋中任意摸出一個小球,記其標有的數字為y,以此確定點M的坐標(x,y).
(1)請你用畫樹狀圖或列表的方法,寫出點M所有可能的坐標;
(2)求點M(x,y)在函數y=﹣![]() 的圖象上的概率.
的圖象上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
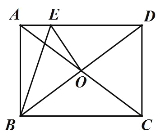
【題目】如圖,矩形 ABCD 的對角線 AC 與 BD 交于點 O,點 E 在 AD 上,且 DE=CD,連接 OE,BE, ABE ![]() ACB ,若 AE=2,則 OE 的長為___________.
ACB ,若 AE=2,則 OE 的長為___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,一次函數y=kx+b與反比例函數y=![]() 的圖象交于A(2,4),B(﹣4,n)兩點.
的圖象交于A(2,4),B(﹣4,n)兩點.
(1)分別求出一次函數與反比例函數的表達式;
(2)過點B作BC⊥x軸,垂足為點C,連接AC,求△ACB的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
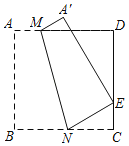
【題目】如圖,把正方形紙片ABCD沿對邊上的兩點M、N所在的直線對折,使點B落在邊CD上的點E處,折痕為MN,其中CE=![]() CD.若AB的長為2,則MN的長為( )
CD.若AB的長為2,則MN的長為( )
A.3B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的對角線相交于O,E是OD的中點,DF∥AC交CE延長線于點F,連接AF.
(1)求證:四邊形AODF是菱形.
(2)若∠AFC=90°,AB=2,求AD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,拋物線y=x2﹣4x+n(x>0)的圖象記為G1,將G1繞坐標原點旋轉180°得到圖象G2,圖象G1和G2合起來記為圖象G.
(1)若點P(﹣1,2)在圖象G上,求n的值.
(2)當n=﹣1時.
①若Q(t,1)在圖象G上,求t的值.
②當k≤x≤3(k<3)時,圖象G對應函數的最大值為5,最小值為﹣5,直接寫出k的取值范圍.
(3)當以A(﹣3,3)、B(﹣3,﹣1)、C(2,﹣1)、D(2,3)為頂點的矩形ABCD的邊與圖象G有且只有三個公共點時,直接寫出n的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com