【題目】如圖，已知拋物線經過點A（﹣1，0），B（3，0），C（0，3）三點．
（1）求此拋物線的解析式；
（2）若點M是線段BC上的點（不與B，C重合），過M作NM∥y軸交拋物線于N，設點M的橫坐標為m，請用含m的代數式表示MN的長；
（3）在（2）的條件下，連接NB，NC，是否存在點M，使△BNC的面積最大？若存在，求m的值；若不存在，請說明理由．
【答案】
（1）解：設拋物線的解析式為：y=a（x+1）（x﹣3），則：
a（0+1）（0﹣3）=3，a=﹣1；
∴拋物線的解析式：y=﹣（x+1）（x﹣3）=﹣x2+2x+3．
（2）解：設直線BC的解析式為：y=kx+b，則有：
，
解得 
；
故直線BC的解析式：y=﹣x+3．
已知點M的橫坐標為m，MN∥y，則M（m，﹣m+3）、N（m，﹣m2+2m+3）；
∴故MN=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m（0＜m＜3）．
（3）解：如圖：
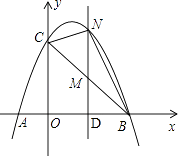
∵S△BNC=S△MNC+S△MNB= 
MN（OD+DB）= MNOB，
∴S△BNC= （﹣m2+3m）3=﹣ 
（m﹣ ）2+ 
（0＜m＜3）；
∴當m= 時，△BNC的面積最大，最大值為 ．
【解析】（1）把ABC 坐標代入解析式即可;（2）豎直線段長等于上縱減下縱，須求BC的解析式；（3）斜三角形（沒有豎直或水平邊）的面積可通過做豎直線分割轉化為豎直三角形（有一條邊豎直邊），即S△BNC=S△MNC+S△MNB，構建函數即可解決.
科目：初中數學 來源： 題型：
【題目】如圖，將方格紙中的△ABC向上平移4個單位長度，然后向右平移6個單位長度，得到△A1B1C1．
（1）畫出平移后的圖形；
（2）線段AA1，BB1的位置關系是______；數量關系是________.
（3）如果每個方格的邊長是1，那么△ABC的面積是___．
查看答案和解析>>
科目：初中數學 來源： 題型：
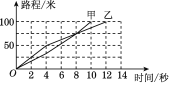
【題目】甲、乙兩人進行比賽的路程與時間的關系如圖所示．
(1)這是一場________米比賽；
(2)前一半賽程內________的速度較快，最終________贏得了比賽；
(3)兩人第________秒在途中相遇，相遇時距終點________米；
(4)甲在前8秒的平均速度是多少？甲在整個賽程的平均速度是多少？乙在前8秒的平均速度是多少？乙在整個賽程的平均速度是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數y=kx+b的圖象分別與反比例函數y= 
的圖象在第一象限交于點A（4，3），與y軸的負半軸交于點B，且OA=OB．
（1）求函數y=kx+b和y= 的表達式；
（2）已知點C（0，5），試在該一次函數圖象上確定一點M，使得MB=MC，求此時點M的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在菱形ABCD中，tan∠ABC= 
，P為AB上一點，以PB為邊向外作菱形PMNB，連結DM，取DM中點E，連結AE，PE，則 
的值為（ ）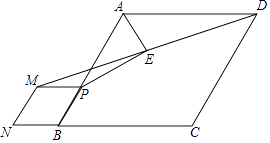
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠A=90°，AB=3，AC=4，D為AC中點，P為AB上的動點，將P繞點D逆時針旋轉90°得到P′，連CP′，則線段CP′的最小值為 ．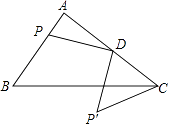 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如下圖時用黑色的正六邊形和白色的正方形按照一定的規律組合而成的兩色圖案
（1）當黑色的正六邊形的塊數為1時，有6塊白色的正方形配套；當黑色的正六邊形塊數為2時，有11塊白色的正方形配套；則當黑色的正六邊形塊數為3，10時，分別寫出白色的正方形配套塊數；
（2）當白色的正方形塊數為201時，求黑色的正六邊形的塊數.
（3）組成白色的正方形的塊數能否為100，如果能，求出黑色的正六邊形的塊數，如果不能，請說明理由
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某學校準備購買若干臺A型電腦和B型打印機.如果購買1臺A型電腦,2臺B型打印機,一共需要花費5900元;如果購買2臺A型電腦,2臺B型打印機,一共需要花費9400元.
(1)求每臺A型電腦和每臺B型打印機的價格分別是多少元?
(2)如果學校購買A型電腦和B型打印機的預算費用不超過20000元,并且購買B型打印機的臺數要比購買A型電腦的臺數多1臺,那么該學校至多能購買多少臺B型打印機?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
