【題目】如圖所示，位于
處的海上救援中心獲悉：在其北偏東
方向的
處有一艘漁船遇險，在原地等待營救．該中心立即把消息告知在其北偏東
相距
海里的
處救生船，并通知救生船，遇險船在它的正東方向處，現救生船沿著航線
前往處救援，若救生船的速度為海里/時，請問：
到
的最短距離是多少？
救生船到達處大約需要多長時間？（結果精確到
小時：參考數據：
，
，
，
，
，
）
【答案】（1）
到
的最短距離是33.51海里，（2）救生船到達B處大約需要1.7小時．
【解析】
（1）根據銳角三角函數可以求得CD和BD的長，從而可以解答本題；
（2）根據（1）中的結果可以解答本題．
（1）過點C作CD⊥AB，垂足為D．
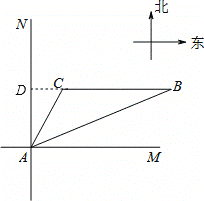
由題意知∠NAC＝30°，∠NAB＝68°，AC＝20，
∴∠CAB＝38°，∠BAM＝90°—68°＝22°，
∵BC∥AM，∴∠CBA＝∠BAM＝22°．
∵CD⊥AB，
∴∠ADC＝∠CDB＝90°．
在Rt△BCD中，sin∠CBD＝
，
∴CB＝
，
（2）救生船到達B處大約需要：t＝
＝1.7(小時)．
答：（1）到的最短距離是33.51海里，（2）救生船到達B處大約需要1.7小時.
科目：初中數學 來源： 題型：
【題目】正方形A1B1C1O、A2B2C2C1、A3B3C3C2…按如圖的方式放置，點A1，A2，A3…和點C1，C2，C3，…分別在直線 y=x+1 和 x 軸上，則點A2019 的坐標是( )
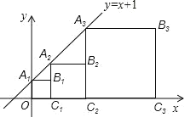
A.(22018 ，22019)B.(22018 1，22018)
C.(22019 ，22018)D.(22018 1，22019 )
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB＝AC，∠A＝120°，BC＝6cm，AB的垂直平分線交BC于點M，交AB于點E，AC的垂直平分線交BC于點N，交AC于點F，則MN的長為多少？
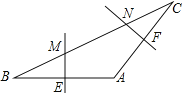
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們知道，任意一個有理數與無理數的和為無理數，任意一個不為零的有理數與一個無理數的積為無理數，而零與無理數的積為零.由此可得：如果mx+n=0，其中m、n為有理數，x為無理數，那么m=0且n=0.
（1）如果
，其中a、b為有理數，那么a= ，b= .
（2）如果
，其中a、b為有理數，求a+2b的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知∠AOB＝60°，OC是∠AOB的平分線，點D為OC上一點，過D作直線DE⊥OA，垂足為點E，且直線DE交OB于點F，如圖所示，若DE＝1，則DF＝_____．
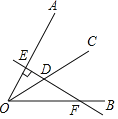
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，等邊三角形ABC中，D為AC上一點，E為AB延長線上一點，DE⊥AC交BC于點F，且DF=EF．
(1)求證：CD=BE；
(2)若AB=12，試求BF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀理解：對于二次三項式a2+2ab+b2，能直接用完全平方公式進行因式分解，得到結果為（a+b）2．而對于二次三項式a2+4ab﹣5b2，就不能直接用完全平方公式了，但我們可采用下述方法：
a2+4ab﹣5b2＝a2+4ab+4b2﹣4b2﹣5b2＝（a+2b）2﹣9b2，
＝（a+2b﹣3b）（a+2b+3b）＝（a﹣b）（a+5b）．
像這樣把二次三項式分解因式的方法叫做添（拆）項法．
解決問趣：
（1）請利用上述方法將二次三項式a2+6ab+8b2分解因式；
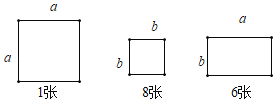
（2）如圖，邊長為a的正方形紙片1張，邊長為b的正方形紙片8張，長為a，寬為b的長方形紙片6張，這些紙片可以拼成一個不重疊，無空隙的長方形圖案，請畫出示意圖；
（3）已知x＞0，且x≠2，試比較分式
與
的大小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下圖是二次函數
的圖象，其頂點坐標為
．
求出圖象與
軸的交點
，
的坐標；
在二次函數的圖象上是否存在點
，使
？若存在，求出點的坐標；若不存在，請說明理由；
將二次函數的圖象在軸下方的部分沿軸翻折，圖象的其余部分保持不變，得到一個新的圖象，請你結合這個新的圖象回答：當直線
與此圖象有兩個公共點時，
的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】關于x的一元二次方程（c+a）x2+2bx+(c-a)=0,其中a、b、c分別為△ABC三邊的長．
（1）如果方程有兩個相等的實數根，試判斷△ABC的形狀并說明理由；
（2）已知a:b:c=3:4:5,求該一元二次方程的根.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com