【題目】為將我們的城市裝扮的更美麗，園林綠化工人要將公園一角的一塊四邊形的空地ABCD種植上花草．經測量，∠B=90°，AB=3米，BC=4米，CD=12米，DA=13米．若每平方米空地需要購買150元的花草．將這塊空地全部綠化需要購買多少元的這種花草？
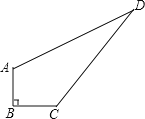
【答案】這塊空地全部綠化需要購買5400元的這種花草．
【解析】
連接AC，在直角三角形ABC中可求得AC的長，由AC、CD、AD的長度關系可得三角形DAC為直角三角形，DA為斜邊；由此看，四邊形ABCD由Rt△ABC和Rt△DAC構成，則容易求解．
連接AC，
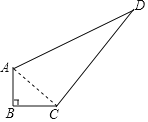
在Rt△ABC中，AC2=AB2+BC2=32+42=52，
在△CAD中，AD2=132，DC2=122，
而122+52=132，
即AC2+CD2=AD2，
∴∠DCA=90°，
S四邊形ABCD=S△BAC+S△DAC=
BCAB+DCAC，
=×4×3+×12×5=36，
所以需費用36×150=5400(元)，
答：這塊空地全部綠化需要購買5400元的這種花草．
科目：初中數學 來源： 題型：
【題目】問題背景
在數學活動課上，張老師要求同學們拿兩張大小不同的矩形紙片進行旋轉變換探究活動．如圖 1，在矩形紙片ABCD 和矩形紙片EFGH中，AB＝1，AD＝2，且FE＞AD，FG＞AB，點E 是 AD 的中點，矩形紙片 EFGH 以點E 為旋轉中心進行逆時針旋轉，在旋轉過程中會產生怎樣的數量關系，提出恰當的數學問題并加以解決．
解決問題
下面是三個學習小組提出的數學問題，請你解決這些問題．
（1）“奮進”小組提出的問題是：如圖 1，當 EF 與 AB 相交于點 M，EH 與 BC 相交于點 N 時，求證：EM=EN．
（2）“雄鷹”小組提出的問題是：在（1）的條件下，當 AM=CN 時，AM 與 BM 有怎樣的數量關系，請說明理由．
（3）“創新”小組提出的問題是：若矩形 EFGH 繼續以點 E 為旋轉中心進行逆時針旋轉，當 
時，請你在圖 2 中畫出旋轉后的示意圖，并求出此時 EF 將邊 BC 分成的兩條線段的長度．
查看答案和解析>>
科目：初中數學 來源： 題型：
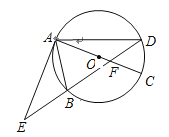
【題目】如圖，⊙O的直徑AC與弦BD相交于點F，點E是DB延長線上一點，∠EAB＝∠ADB.
(1)求證：EA是⊙O的切線；
(2)已知點B是EF的中點，AF＝4，CF＝2，求AE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某學校一班級開展為貧困山區學生捐錢助學活動，該班有20名學生捐出了自己的零花錢，捐款數如下：(單位：元)
19 | 20 | 25 | 30 | 28 | 27 | 26 | 21 | 20 | 22 | 24 | 23 | 25 | 29 | 27 | 28 | 27 | 30 | 19 | 20 |
該班老師準備將此次活動的捐款數據制成頻數分布直方圖，在制圖時請你幫老師算出以下數據：
(1)計算最大值與最小值的差；
(2)若選定組距為2計算將這20個數據分成的組數；并計算將第一組的起點定為18.5時捐款數在26.5-28.5范圍內的頻數；
(3)計算第一組和最后一組這兩個組內包含的所有樣本的平均數
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，方格紙中每個小方格都是邊長為1的正方形，已知學校的坐標為A(2，2)．
(1)請在圖中建立適當的直角坐標系，并寫出圖書館的坐標；
(2)若體育館的坐標為C(－2，3)，請在坐標系中標出體育館的位置，并順次連接學校、圖書館、體育館，得到△ABC，求△ABC的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
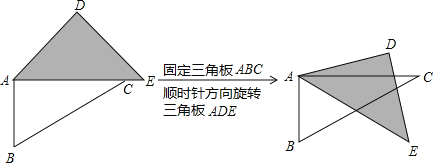
【題目】如圖1，將三角板ABC與三角板ADE擺放在一起；如圖2，固定三角板ABC，將三角板ADE繞點A按順時針方向旋轉，記旋轉角∠CAE=α（0°＜α＜180°）．當△ADE的一邊與△ABC的某一邊平行（不共線）時，寫出旋轉角α的所有可能的度數為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，已知直線AB和CD相交于點O，OM平分∠BOD，∠MON＝90°，∠AOC＝50°．
（1）求∠AON的度數．
（2）寫出∠DON的余角．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場購進一批LED燈泡與普通白熾燈炮，其進價與標價如下表，該商場購進LED燈泡與普通白熾燈炮共300個，LED燈泡按標價進行銷售，而普通白熾燈炮按標價打九折銷售，銷售完這批燈泡后可以獲利3200元。
（1）求該商場購進LED燈泡與普通白熾燈泡的數量分別為多少個？
（2）由于春節期間熱銷，很快將兩種燈泡銷售完，若該商場計劃再次購進兩種燈泡120個，并在不打折的情況下銷售完，若銷售完這批燈泡的獲利不超過總進貨價的28％，則最多購進LED燈泡多少個？
LED燈泡 | 普通白熾燈泡 | |
進價（元） | 45 | 25 |
標價（元） | 60 | 30 |
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線AB過x軸上一點A（2，0），且與拋物線y=ax2相交于B、C兩點，B點坐標為（1，1）．
（1）求直線AB的解析式及拋物線y=ax2的解析式；
（2）求點C的坐標；
（3）求S△COB．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com