
【題目】問題提出
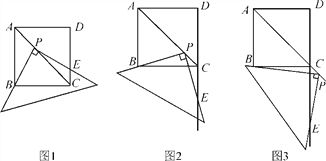
(1)如圖1,將直角三角板的直角頂點P放在正方形ABCD的對角線AC上,一條直角邊經過點B,另一條直角邊交邊DC于點E,線段PB和線段PE相等嗎?請證明;
問題探究
(2)如圖2,移動三角板,使三角板的直角頂點P在對角線AC上,一條直角邊經過點B,另一條直角邊交DC的延長線于點E,(1)中的結論還成立嗎?若成立,請證明;若不成立,請說明理由;
問題解決
(3)繼續移動三角板,使三角板的直角頂點P在對角線AC上,一條直角邊經過點B,另一條直角邊交DC的延長線于點E,(1)中的結論還成立嗎?若成立,請證明;若不成立,請說明理由.
【答案】(1)證明見解析(2)PB=PE還成立(3) PB=PE還成立
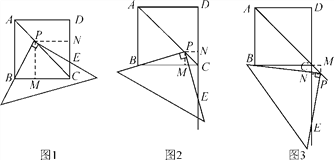
【解析】試題分析:(1)根據正方形的性質得∠BCD=90°,AC平分∠BCD,而PM⊥CD,則四邊形PMCN是矩形,根據角平分線的性質可得PM=PN,根據四邊形的內角和得到∠PBC+∠CEP=180°,再利用等角的補角相等得到∠PBM=∠PEN,然后根據AAS證明△PBM≌△PEN,則可證明;
(2)連接PD,根據正方形的性質和角平分線的性質,由“SAS”以及四邊形的內角和得證;
(3)過點P作PM⊥BC,PN⊥CD,然后根據角平分線的性質和正方形的性質,由“AAS”可證.
試題解析:(1)如圖1,過點P作PM⊥BC,PN⊥CD,垂足分別為M,N,∵四邊形ABCD為正方形,∴∠BCD=90°,AC平分∠BCD,∵PM⊥BC,PN⊥CD,∴四邊形PMCN為正方形,PM=PN,∵∠BPE=90°,∠BCD=90°,∴∠PBC+∠CEP=180°,而∠CEP+∠PEN=180°,∴∠PBM=∠PEN,在△PBM和△PEN中, 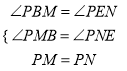 ∴△PBM≌△PEN(AAS),∴PB=PE (2)如圖2,PB=PE還成立.理由如下:過點P作PM⊥BC,PN⊥CD,垂足分別為M,N,∵四邊形ABCD為正方形,∴∠BCD=90°,AC平分∠BCD,∵PM⊥BC,PN⊥CD,∴四邊形PMCN為正方形,PM=PN,∴∠MPN=90°,∵∠BPE=90°,∠BCD=90°,∴∠BPM+∠MPE=90°,而∠MPE+∠EPN=90°,∴∠BPM=∠EPN,在△PBM和△PEN中,
∴△PBM≌△PEN(AAS),∴PB=PE (2)如圖2,PB=PE還成立.理由如下:過點P作PM⊥BC,PN⊥CD,垂足分別為M,N,∵四邊形ABCD為正方形,∴∠BCD=90°,AC平分∠BCD,∵PM⊥BC,PN⊥CD,∴四邊形PMCN為正方形,PM=PN,∴∠MPN=90°,∵∠BPE=90°,∠BCD=90°,∴∠BPM+∠MPE=90°,而∠MPE+∠EPN=90°,∴∠BPM=∠EPN,在△PBM和△PEN中, 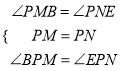 ∴△PBM≌△PEN(ASA),∴PB=PE (3)如圖3,PB=PE還成立.理由如下:過點P作PM⊥BC交BC的延長線于點M,PN⊥CD的延長線于點N,∵四邊形ABCD為正方形,∴∠BCD=90°,AC平分∠BCD,∵PM⊥BC,PN⊥CD,∴四邊形PMCN為正方形,PM=PN,∴∠MPN=90°,∵∠BPE=90°,∠BCD=90°,∴∠BPM+∠BPN=90°,而∠BPN+∠EPN=90°,∴∠BPM=∠EPN,在△PBM和△PEN中,
∴△PBM≌△PEN(ASA),∴PB=PE (3)如圖3,PB=PE還成立.理由如下:過點P作PM⊥BC交BC的延長線于點M,PN⊥CD的延長線于點N,∵四邊形ABCD為正方形,∴∠BCD=90°,AC平分∠BCD,∵PM⊥BC,PN⊥CD,∴四邊形PMCN為正方形,PM=PN,∴∠MPN=90°,∵∠BPE=90°,∠BCD=90°,∴∠BPM+∠BPN=90°,而∠BPN+∠EPN=90°,∴∠BPM=∠EPN,在△PBM和△PEN中,  ∴△PBM≌△PEN(ASA),∴PB=PE
∴△PBM≌△PEN(ASA),∴PB=PE


科目:初中數學 來源: 題型:
【題目】《九章算術》中有一道闡述“盈不足術”的問題,原文如下:今有人共買物,人出八,盈三;人出七,不足四.問人數幾何?譯文為:現有一些人共同買一個物品,每人出8元,還盈余3元;每人出7元,則還差4元,問共有_____人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P是拋物線y=﹣x2+x+2在第一象限上的點,過點P分別向x軸和y軸引垂線,垂足分別為A,B,則四邊形OAPB周長的最大值為_____.
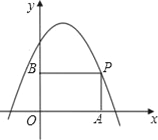
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在6×6的正方形網格中,每個小正方形的邊長都為1,請在所給網格中按下列要求畫出圖形.

(1)從點A出發的一條線段AB,使它的另一個端點落在格點(即小正方形的頂點)上,且長度為![]() ;
;
(2)以(1)中的AB為邊的一個等腰三角形ABC,使點C在格點上,請畫出所有滿足條件的點C.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班為了獎勵在學校體育運動會中表現突出的同學,班主任派生活委員小明到文具店為獲獎的同學買獎品,小明發現,如果買1本筆記本和3支鋼筆,則需要19元;如果買2本筆記本和5支鋼筆,則需要33元.
(1)求購買每本筆記本和每支鋼筆各多少元?
(2)班主任給小明的班費只有110元,要獎勵24名同學每人一件獎品,則小明至少要購買多少本筆記本?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在長方形ABCD中,AB=6,BC=8
(1)求對角線AC的長;
(2)點E是線段CD上的一點,把△ADE沿著直線AE折疊.點D恰好落在線段AC上,點F重合,求線段DE的長. 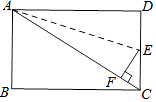
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com