
【題目】對于平面內的點![]() 和點
和點![]() ,給出如下定義:點
,給出如下定義:點![]() 為平面內的一點,若點
為平面內的一點,若點![]() 使得
使得![]() 是以
是以![]() 為頂角且
為頂角且![]() 小于90°的等腰三角形,則稱點
小于90°的等腰三角形,則稱點![]() 是點
是點![]() 關于點
關于點![]() 的銳角等腰點
的銳角等腰點![]() .如圖,點
.如圖,點![]() 是點
是點![]() 關于點
關于點![]() 的銳角等腰點.在平面直角坐標系
的銳角等腰點.在平面直角坐標系![]() 中,點
中,點![]() 是坐標原點.
是坐標原點.

(1)已知點![]() ,在點
,在點![]() ,
,![]() 中,是點
中,是點![]() 關于點
關于點![]() 的銳角等腰點的是___________.
的銳角等腰點的是___________.
(2)已知點![]() ,點
,點![]() 在直線
在直線![]() 上,若點
上,若點![]() 是點
是點![]() 關于點
關于點![]() 的銳角等腰點,求實數
的銳角等腰點,求實數![]() 的取值范圍.
的取值范圍.
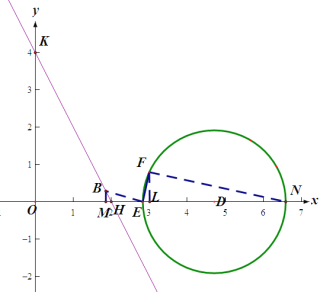
(3)點![]() 是
是![]() 軸上的動點,
軸上的動點,![]() ,點
,點![]() 是以
是以![]() 為圓心,2為半徑的圓上一個動點,且滿足
為圓心,2為半徑的圓上一個動點,且滿足![]() .直線
.直線![]() 與
與![]() 軸和
軸和![]() 軸分別交于點
軸分別交于點![]() ,若線段
,若線段![]() 上存在點
上存在點![]() 關于點
關于點![]() 的銳角等腰點,請直接寫出
的銳角等腰點,請直接寫出![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據等腰銳角點的定義即得;
(2)先確定極限位置:直線與圓相切于第四象限及直線過(0,3)時b的值,進而確定范圍;
(3)分類討論:E點和F點位于線段HK左側;E點和F點位于線段HK右側;利用一線三垂直模型及相似三角形的性質確定極限位置t的值,進而確定范圍.
(1)∵點P是點![]() 關于點
關于點![]() 的銳角等腰點,
的銳角等腰點,![]()
∴OA=OP=2
如下圖:
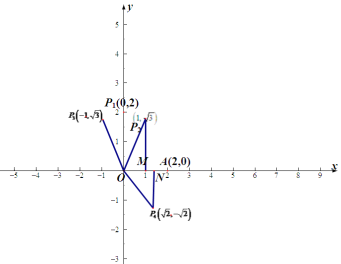
當![]() 時,OP1=2,OP1⊥OA,不成立;
時,OP1=2,OP1⊥OA,不成立;
當![]() 時,過P2作P2M⊥x軸
時,過P2作P2M⊥x軸
∴OM=1,P2M=![]()
∴在![]() 中,
中,![]()
∵![]()
∴點![]() 是點
是點![]() 關于點
關于點![]() 的銳角等腰點;
的銳角等腰點;
當![]() 時,
時,![]()
∴點![]() 不是點
不是點![]() 關于點
關于點![]() 的銳角等腰點;
的銳角等腰點;
當![]() 時,過P4作P4N⊥x軸
時,過P4作P4N⊥x軸
∴ON=![]() ,P4N=
,P4N=![]()
∴在![]() 中,
中,![]() ,
,![]()
∴點![]() 是點
是點![]() 關于點
關于點![]() 的銳角等腰點.
的銳角等腰點.
∴點![]() 關于點
關于點![]() 的銳角等腰點有
的銳角等腰點有![]() ,
,![]()
故答案為:![]()
(2)以O為圓心,OA=3為半徑作圓,當直線![]() 與圓O相切與第四象限時,切點即為點
與圓O相切與第四象限時,切點即為點![]() 關于點
關于點![]() 的銳角等腰點,如下圖點
的銳角等腰點,如下圖點![]() .
.
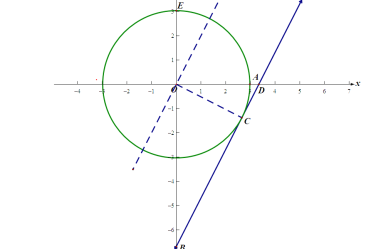
由題意,得:OB=-b,OD=![]()
∴在![]() 中,
中,![]()
∵![]()
∴![]()
解得:![]()
如上圖:當直線![]() 過點E
過點E![]() 時,
時,![]() ,OE⊥OA
,OE⊥OA
∴要使在直線![]() 上存在點
上存在點![]() 是點
是點![]() 關于點
關于點![]() 的銳角等腰點,
的銳角等腰點,![]()
綜上所述:![]() 時,直線
時,直線![]() 上存在點
上存在點![]() 是點
是點![]() 關于點
關于點![]() 的銳角等腰點 .
的銳角等腰點 .
(3)如下圖:
當![]() 在直線左側,
在直線左側,![]() 時,過
時,過![]() 作
作![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴KO=4,KH=![]() ,EH=4-t
,EH=4-t
∴EG=![]()
∵要使線段![]() 上存在點
上存在點![]() 關于點
關于點![]() 的銳角等腰點,則
的銳角等腰點,則![]()
∴![]()
∴![]()
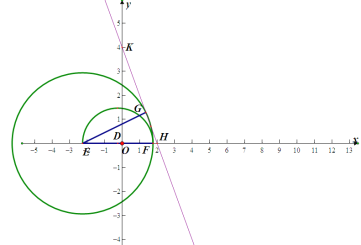
當E點和F點位于線段HK右側時,即:![]() 時,如下圖,過E作EB⊥EF,過B作BM⊥x軸,過點F作FL⊥x軸
時,如下圖,過E作EB⊥EF,過B作BM⊥x軸,過點F作FL⊥x軸
當![]() 時,
時,![]()
∴![]() ,
,![]()
∵![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
∴![]()
將點![]() 代入直線
代入直線![]() 得:
得:
![]()
解得:![]()
∴當![]() 時,線段
時,線段![]() 上存在點
上存在點![]() 關于點
關于點![]() 的銳角等腰點.
的銳角等腰點.
∵![]() ,
,![]()
∴![]() ,即
,即![]()
綜上所述:![]() 時,線段
時,線段![]() 上存在點
上存在點![]() 關于點
關于點![]() 的銳角等腰點
的銳角等腰點


科目:初中數學 來源: 題型:
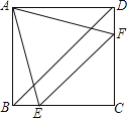
【題目】如圖,在正方形ABCD中,邊長為2的等邊三角形AEF的頂點E,F分別在BC和CD上,下列結論:①CE=CF;②BD=1+![]() ;③BE+DF=EF;④∠AEB=75°.其中正確的序號是______.
;③BE+DF=EF;④∠AEB=75°.其中正確的序號是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線M:y=-x2+2bx+c與直線l:y=9x+14交于點A,其中點A的橫坐標為-2.
(1)請用含有b的代數式表示c: ;
(2)若點B在直線l上,且B的橫坐標為-1,點C的坐標為(b,5).
①若拋物線M還過點B,直接寫出該拋物線的解析式;
②若拋物線M與線段BC恰有一個交點,結合函數圖象,直接寫出b的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,函數![]() (x>0)的圖象與直線l1:
(x>0)的圖象與直線l1:![]() 交于點A,與直線l2:x=k交于點B.直線l1與l2交于點C.
交于點A,與直線l2:x=k交于點B.直線l1與l2交于點C.

(1) 當點A的橫坐標為1時,則此時k的值為 _______;
(2) 橫、縱坐標都是整數的點叫做整點. 記函數![]() (x>0) 的圖像在點A、B之間的部分與線段AC,BC圍成的區域(不含邊界)為W.
(x>0) 的圖像在點A、B之間的部分與線段AC,BC圍成的區域(不含邊界)為W.
①當k=3時,結合函數圖像,則區域W內的整點個數是_________;
②若區域W內恰有1個整點,結合函數圖象,直接寫出k的取值范圍:___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,函數![]() 的圖象G經過點
的圖象G經過點![]() ,直線
,直線![]() 與y軸交于點B,與圖象G交于點C.
與y軸交于點B,與圖象G交于點C.
(1)求m的值.
(2)橫、縱坐標都是整數的點叫做整點.記圖象G在點A,C之間的部分與線段BA,BC圍成的區域(不含邊界)為W.
①當直線l過點![]() 時,直接寫出區域W內的整點個數.
時,直接寫出區域W內的整點個數.
②若區域W內的整點不少于4個,結合函數圖象,求k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
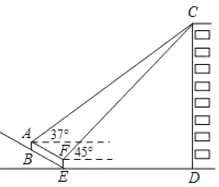
【題目】我校數學興趣小組的同學要測量建筑物![]() 的高度,如圖,建筑物
的高度,如圖,建筑物![]() 前有一段坡度為
前有一段坡度為![]() 的斜坡
的斜坡![]() ,小明同學站在斜坡上的
,小明同學站在斜坡上的![]() 點處,用測角儀測得建筑物屋頂
點處,用測角儀測得建筑物屋頂![]() 的仰角為
的仰角為![]() ,接著小明又向下走了
,接著小明又向下走了![]() 米,剛好到達坡底
米,剛好到達坡底![]() 處,這時測到建筑物屋頂
處,這時測到建筑物屋頂![]() 的仰角為
的仰角為![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 在同一平面內.若測角儀的高度
在同一平面內.若測角儀的高度![]() 米,則建筑物
米,則建筑物![]() 的高度約為( ).(精確到0.1米,參考數據:
的高度約為( ).(精確到0.1米,參考數據:![]() ,
,![]() ,
,![]() )
)
A.38.6B.39.0C.40.0D.41.5
查看答案和解析>>
科目:初中數學 來源: 題型:
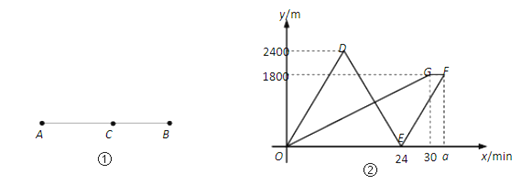
【題目】如圖①,點A表示小明家,點B表示學校.小明媽媽騎車帶著小明去學校,到達C處時發現數學書沒帶,于是媽媽立即騎車原路回家拿書后再追趕小明,同時小明步行去學校,到達學校后等待媽媽.假設拿書時間忽略不計,小明和媽媽在整個運動過程中分別保持勻速.媽媽從C處出發x分鐘時離C處的距離為y1米,小明離C處的距離為y2米,如圖②,折線O-D-E-F表示y1與x的函數圖像;折線O-G-F表示y2與x的函數圖像.
(1)小明的速度為 m/min,圖②中a的值為 .
(2)設媽媽從C處出發x分鐘時媽媽與小明之間的距離為y米.當12≤x≤30時,求出y與x的函數表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】體育老師為了解本校九年級女生1分鐘“仰臥起坐”體育測試項目的達標情況,從該校九年級136名女生中,隨機抽取了20名女生,進行了1分鐘仰臥起坐測試,獲得數據如下:
收集數據:抽取20名女生的1分鐘仰臥起坐測試成績(個)如下:
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
(1)整理、描述數據:請你按如下分組整理、描述樣本數據,把下列表格補充完整:
范圍 |
|
|
|
|
|
|
|
人數 |
(說明:每分鐘仰臥起坐個數達到49個及以上時在中考體育測試中可以得到滿分)
(2)分析數據:樣本數據的平均數、中位數、滿分率如下表所示:
平均數 | 中位數 | 滿分率 |
46.8 | 47.5 |
|
得出結論:①估計該校九年級女生在中考體育測試中1分鐘“仰臥起坐”項目可以得到滿分的人數;
②該中心所在區縣的九年級女生的1分鐘“仰臥起坐”總體測試成績如下:
平均數 | 中位數 | 滿分率 |
45.3 | 49 |
|
請你結合該校樣本測試成績和該區縣總體測試成績,為該校九年級女生的1分鐘“仰臥起坐”達標情況做一下評估.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com