
【題目】一、閱讀理解:
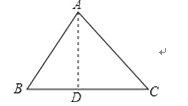
在△ABC中,BC=a,CA=b,AB=c;
(1)若∠C為直角,則a2+b2=c2;
(2)若∠C為銳角,則a2+b2與c2的關系為:a2+b2>c2;
(3)若∠C為鈍角,試推導a2+b2與c2的關系.
二、探究問題:在△ABC中,BC=a=3,CA=b=4,AB=c,若△ABC是鈍角三角形,求第三邊c的取值范圍.
【答案】一、(1)a2+b2=c2;(2)a2+b2>c2;(3)a2+b2<c2;
二、5<c<7或1<c<![]() .
.
【解析】
試題分析:一、(1)由勾股定理即可得出結論;
(2)作AD⊥BC于D,則BD=BC﹣CD=a﹣CD,由勾股定理得出AB2﹣BD2=AD2,AC2﹣CD2=AD2,得出AB2﹣BD2=AC2﹣CD2,整理得出a2+b2=c2+2aCD,即可得出結論;
(3)作AD⊥BC于D,則BD=BC+CD=a+CD,由勾股定理得出AD2=AB2=BD2,AD2=AC2﹣CD2,得出AB2﹣BD2=AC2﹣CD2,整理即可得出結論;
二、分兩種情況:①當∠C為鈍角時,由以上(3)得:![]() <c<a+b,即可得出結果;②當∠B為鈍角時,得:b﹣a<c<
<c<a+b,即可得出結果;②當∠B為鈍角時,得:b﹣a<c<![]() ,即可得出結果.
,即可得出結果.
試題解析:一、解:(1)∵∠C為直角,BC=a,CA=b,AB=c,
∴a2+b2=c2;
(2)作AD⊥BC于D,如圖1所示:
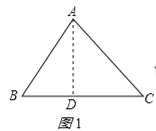
則BD=BC﹣CD=a﹣CD,
在△ABD中,AB2﹣BD2=AD2,
在△ACD中,AC2﹣CD2=AD2,
∴AB2﹣BD2=AC2﹣CD2,
∴c2﹣(a﹣CD)2=b2﹣CD2,
整理得:a2+b2=c2+2aCD,
∵a>0,CD>0,
∴a2+b2>c2;
(3)作AD⊥BC于D,如圖2所示:
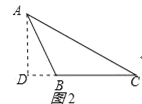
則BD=BC+CD=a+CD,
在△ABD中,AD2=AB2=BD2,
在△ACD中,AD2=AC2﹣CD2,
∴AB2﹣BD2=AC2﹣CD2,
∴c2﹣(a+CD)2=b2﹣CD2,
整理得:a2+b2=c2﹣2aCD,
∵a>0,CD>0,
∴a2+b2<c2;
二、解:當∠C為鈍角時,由以上(3)得:![]() <c<a+b,
<c<a+b,
即5<c<7;
當∠B為鈍角時,得:b﹣a<c<![]() ,
,
即1<c<![]() ;
;
綜上所述:第三邊c的取值范圍為5<c<7或1<c<![]() .
.


 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:初中數學 來源: 題型:
【題目】下列命題中,正確命題的序號是:
①一組對邊平行且相等的四邊形是平行四邊形;
②一組鄰邊相等的平行四邊形是正方形;
③對角線相等的四邊形是矩形;
④三角形的外心到三角形各頂點的距離相等。
A. ①②B. ②③C. ③④D. ①④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列各條件中,能作出唯一的△ABC的是( )
A. AB=4,BC=5,AC=10 B. AB=5,BC=4,∠A=40°
C. ∠A=90°,AB=10 D. ∠A=60°,∠B=50°,AB=5
查看答案和解析>>
科目:初中數學 來源: 題型:
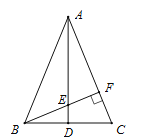
【題目】如圖,在△ABC中,AB=AC,點D是BC的中點,點E在AD上,BE的延長線交AC于點F,且BF⊥AC,垂足為F,∠BAC=45°
求證:△AEF≌△BCF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x,y的方程組![]() . 給出下列結論:
. 給出下列結論:
①![]() 是方程組的解;②當k=
是方程組的解;②當k=![]() 時,x ,y的值互為相反數;
時,x ,y的值互為相反數;
③若方程組的解也是方程x + y =4 – k的解,則k=1;
④若![]() ,則
,則![]() . 其中正確的是________。
. 其中正確的是________。
查看答案和解析>>
科目:初中數學 來源: 題型:
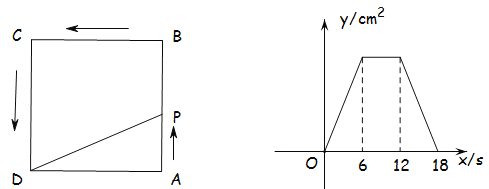
【題目】如圖①,在正方形![]() 中,點
中,點![]() 以
以![]() 的速度從點
的速度從點![]() 出發按箭頭方向運動,到達點
出發按箭頭方向運動,到達點![]() 停止.
停止. ![]() 的面積
的面積![]() 與運動時間
與運動時間![]() 之間的函數圖像如圖②所示.(規定:點
之間的函數圖像如圖②所示.(規定:點![]() 在點
在點![]() ,
, ![]() 時,
時, ![]() )
)
發現:(1) ![]() = _______
= _______ ![]() ,當
,當![]() 時,
時, ![]() =_________
=_________ ![]() ;
;
(2)當點![]() 在線段_________上運動時,
在線段_________上運動時, ![]() 的值保持不變.
的值保持不變.
拓展:求當![]() 及
及![]() 時,
時, ![]() 與
與![]() 之間的函數關系式.
之間的函數關系式.
探究:當![]() 為多少時,
為多少時, ![]() 的值為
的值為![]() ?
?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com