
【題目】如圖,在矩形ABCD中,AB=2,BC=4,點M、N分別在邊AD和BC上,沿MN折疊四邊形ABCD,使點A、B分別落在A1、B1處,得四邊形A1B1NM,其中點B1在DC上,過點M作ME⊥BC于點E,連接BB1 , 給出下列結論:①∠MNB1=∠ABB1;②△MEN∽△BCB1;③ ![]() 的值為定值;④當B1C=
的值為定值;④當B1C= ![]() DC時,AM=
DC時,AM= ![]() ,其中正確結論的序號是 . (把所有正確結論的序號都在填在橫線上)
,其中正確結論的序號是 . (把所有正確結論的序號都在填在橫線上) 
【答案】①②③
【解析】解:由折疊可知∠MNB1=∠BNM,MN⊥BB1,
∴∠BNM+∠B1BN=90°,
∵∠ABB1+∠B1BN=90°,
∴∠BNM=∠ABB1,
∴∠MNB1=∠ABB1,故①正確;
∵ME⊥BC,
∴∠MNE+∠NME=90°,
由由折疊的性質可得MN⊥BB1,
∴∠MNE+∠B1BN=90°,
∴∠NME=∠BB1N,
∴△MEN∽△BCB1,
故②正確;
由②可知 ![]() =
= ![]() ,
,
∵ME=AB=2,BC=4,
∴ ![]() =
= ![]() =
= ![]() ,為定值,故③正確;
,為定值,故③正確;
∵△MEN∽△BCB1,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴NE= ![]() B1C,
B1C,
若B1C= ![]() DC,
DC,
則NE= ![]() DC=
DC= ![]() ×2=
×2= ![]() ,
,
設BN=x,則NC=4﹣x,B1N=x,
在Rt△B1NC中,由勾股定理可得x2=(4﹣x)2+12,
解得x= ![]() ,
,
∴AM=BE=BN﹣NE= ![]() ﹣
﹣ ![]() =
= ![]() ,故④不正確.
,故④不正確.
所以答案是:①②③.
【考點精析】根據題目的已知條件,利用矩形的性質和翻折變換(折疊問題)的相關知識可以得到問題的答案,需要掌握矩形的四個角都是直角,矩形的對角線相等;折疊是一種對稱變換,它屬于軸對稱,對稱軸是對應點的連線的垂直平分線,折疊前后圖形的形狀和大小不變,位置變化,對應邊和角相等.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,OA⊥OB,AB⊥x軸于點C,點A( ![]() ,1)在反比例函數y=
,1)在反比例函數y= ![]() (x≠0)的圖象上.
(x≠0)的圖象上.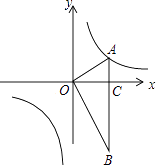
(1)求反比例函數y= ![]() (x≠0)的解析式和點B的坐標;
(x≠0)的解析式和點B的坐標;
(2)若將△BOA繞點B按逆時針方向旋轉60°得到△BDE(點O與點D是對應點),補全圖形,直接寫出點E的坐標,并判斷點E是否在該反比例函數的圖象上,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了響應“中小學生每天鍛煉1小時”的號召,某校開展了形式多樣的“陽光體育”活動,小明對某班同學參加鍛煉的情況進行了調查與統計,并繪制了下面的圖1與圖2.根據你對圖1與圖2的理解,回答下列問題:
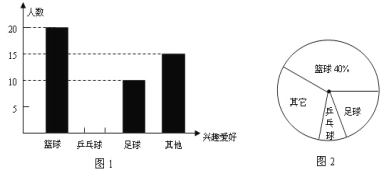
(1)小明調查的這個班級有多少名學生,參加足球鍛煉的學生人數所占的百分比是多少?
(2)請你將圖1中“乒乓球”部分補充完整.
(3)求出扇形統計圖中表示“足球”的扇形的圓心角的度數.
(4)若這個學校共有1200名學生,估計參加乒乓球活動的學生有多少名學生?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,某公路檢測中心在一事故多發地帶安裝了一個測速儀,檢測點設在距離公路10m的A處,測得一輛汽車從B處行駛到C處所用的時間為0.9秒.已知∠B=30°,∠C=45°

(1)求B,C之間的距離;(保留根號)
(2)如果此地限速為80km/h,那么這輛汽車是否超速?請說明理由.(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場二樓擺出一臺游戲裝置如圖所示,小球從最上方入口處投入,每次遇到黑色障礙物,等可能地向左或向右邊落下.
(1)若樂樂投入一個小球,則小球落入B區域的概率為 .
(2)若樂樂先后投兩個小球,求兩個小球同時落在A區域的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,∠B=90°,AB∥CD,M為BC邊上的一點,且AM平分∠BAD,DM平分∠ADC.
求證:(1)AM⊥DM;
(2)M為BC的中點.
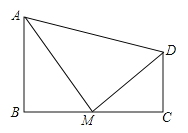
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() ,對角線AC、BD相交于點O.
,對角線AC、BD相交于點O.
⑴若AB=BC,則![]() 是_______.
是_______.
⑵若AC=BD,則![]() 是_________.
是_________.
⑶若∠BCD=90°,則![]() 是_________.
是_________.
⑷若OA=OB,且OA⊥OB,則![]() 是_________.
是_________.
⑸若AB=BC,且AC=BD,則![]() 是_________.
是_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司銷售部有營銷人員15人,銷售部為了制定某種商品的月銷售定額,統計了這15人某月的銷售如下:
每人銷售件數 | 1800 | 510 | 250 | 210 | 150 | 120 |
人數 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求這15位營銷人員該月銷售量的平均數、中位數和眾數.
(2)假設銷售部負責人把每位營銷員的月銷售額定為320件,你認為是否合理?為什么?如不合理,請你制定一個合理的銷售定額,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com