
【題目】直線AB:y=-x+b分別與x,y軸交于A(8,0)、B兩點,過點B的直線交x軸軸負半軸于C,且OB:OC=4:3.
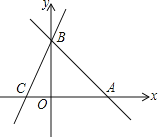
(1)求點B的坐標為 __________;
(2)求直線BC的解析式;
(3)動點M從C出發沿射線CA方向運動,運動的速度為每秒1個單位長度.設M運動t秒時,當t為何值時△BCM為等腰三角形.
【答案】(1)B(0,8);(2) y=![]() x+8;(3)10秒、
x+8;(3)10秒、![]() 秒或12秒.
秒或12秒.
【解析】試題分析:(1)把A的坐標代入y=-x+b,可得AB的解析式,令x=0,求出y的值,可得B的坐標;
(2)根據OB:OC=4:3,可得OC的長,根據待定系數法,可得函數解析式;
(3)根據等腰三角形的定義,分類討論:MC=BC,MC=MB,BC=BM,①當MC=BC時,根據路程處以速度等于時間,可得答案;②當MC=MB時,根據兩點間的距離,可得關于a的方程,根據解方程,可得a的值,再根據路程除以速度等于時間,可得答案;③當BC=BM時,根據線段垂直平分線的性質,可得MO的長,再根據兩點間的距離,可得MC的長,根據路程除以速度等于時間,可得答案.
試題解析:解:(1)y=﹣x+b分別與x軸交于A(8、0),得:﹣8+b=0.解得b=8,即函數解析式為y=﹣x+8,當x=0時,y=8,B點坐標是(0,8);
(2)由OB:OC=4:3,BC=8,得:8:BC=4:3,解得BC=6,即C(﹣6,0),設直線BC的解析式為y=kx+b,圖象經過點B,C,得: ![]() ,解得:
,解得: 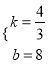 ,∴直線BC的解析式為y=
,∴直線BC的解析式為y=![]() x+8;
x+8;
(3)設M點坐標(a,0),由勾股定理得:BC=![]() =10,分三種情況討論:
=10,分三種情況討論:
①當MC=BC=10時,由路程處以速度等于時間,得10÷1=10(秒),即M運動10秒,△BCM為等腰三角形;
②當MC=MB時,MC2=MB2,即(a+6)2=a2+82,化簡,得12a=28,解得a=![]() 即M(
即M(![]() ,0).MC=
,0).MC=![]() ﹣(﹣6)=
﹣(﹣6)=![]() +6=
+6=![]() ,由路程除以速度等于時間,得
,由路程除以速度等于時間,得![]() ÷1=
÷1=![]() (秒),即M運動
(秒),即M運動![]() 秒時,△BCM為等腰三角形;
秒時,△BCM為等腰三角形;
③當BC=BM時,得OC=OM=6,即MC=6﹣(﹣6)=6+6=12,由路程除以速度等于時間,得12÷1=12(秒),即M運動12秒時,△BCM為等腰三角形.
綜上所述:t=10(秒),t=![]() (秒),t=12(秒)時,△BCM為等腰三角形.
(秒),t=12(秒)時,△BCM為等腰三角形.


 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線AB與直線CD相交于點O,EO⊥AB,OF平分∠AOC, 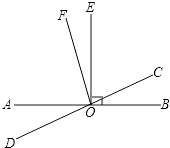
(1)請寫出∠EOC的余角;
(2)若∠BOC=40°,求∠EOF的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把Rt△ABC放在直角坐標系內,其中∠CAB=90°,BC=5,點A,B的坐標分別為(1,0),(4,0),將△ABC沿x軸向右平移,當點C落在直線y=2x-6上時,線段BC掃過的面積為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在如圖所示的方格紙中,每個小方格都是邊長為1個單位的正方形,圖①、圖②、圖③均為頂點都在格點上的三角形(每個小方格的頂點叫格點),
(1)在圖1中,圖①經過一次 變換(填“平移”或“旋轉”或“軸對稱”)可以得到圖②;
(2)在圖1中,圖③是可以由圖②經過一次旋轉變換得到的,其旋轉中心是點 (填“A”或 “B”或“C”);
(3)在圖2中畫出圖①繞點A順時針旋轉90°后的圖④.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB的垂直平分線MN交AB于點E,交AC于點D,且AC=15cm,△BCD的周長等于25cm. 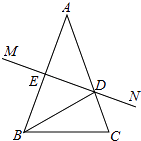
(1)求BC的長;
(2)若∠A=36°,并且AB=AC,求證:BC=BD.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com