
【題目】如圖,AB為⊙O的直徑,AC、DC為弦,∠ACD=60°,P為AB延長線上的點,∠APD=30°. 
(1)求證:DP是⊙O的切線;
(2)若⊙O的半徑為3cm,求圖中陰影部分的面積.
【答案】
(1)證明:連接OD,
∵∠ACD=60°,
∴由圓周角定理得:∠AOD=2∠ACD=120°,
∴∠DOP=180°﹣120°=60°,
∵∠APD=30°,
∴∠ODP=180°﹣30°﹣60°=90°,
∴OD⊥DP,
∵OD為半徑,
∴DP是⊙O切線
(2)解:∵∠P=30°,∠ODP=90°,OD=3cm,
∴OP=6cm,由勾股定理得:DP=3 ![]() cm,
cm,
∴圖中陰影部分的面積S=S△ODP﹣S扇形DOB= ![]() ×3×3
×3×3 ![]() ﹣
﹣ ![]() =(
=( ![]()
![]() ﹣
﹣ ![]() π)cm2
π)cm2

【解析】(1)連接OD,求出∠AOD,求出∠DOB,求出∠ODP,根據切線判定推出即可;(2)求出OP、DP長,分別求出扇形DOB和三角形ODP面積,即可求出答案.


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點D、E分別在邊AB、AC上,如果DE∥BC,且∠DCE=∠B,那么下列說法中,錯誤的是( ) 
A.△ADE∽△ABC
B.△ADE∽△ACD
C.△ADE∽△DCB
D.△DEC∽△CDB
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司研發了一款成本為60元的保溫飯盒,投放市場進行試銷售,按物價部門規定,其銷售單價不低于成本,但銷售利潤不高于65%,市場調研發現,保溫飯盒每天的銷售數量y(個)與銷售單價x(元)滿足一次函數關系;當銷售單價為70元時,銷售數量為160個;當銷售單價為80元時,銷售數量為140個(利潤率= ![]() )
)
(1)求y與x之間的函數關系式;
(2)當銷售單價定為多少元時,公司每天獲得利潤最大,最大利潤為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為4的正方形ABCD中,動點P從A點出發,以每秒1個單位長度的速度沿AB向B點運動,同時動點Q從B點出發,以每秒2個單位長度的速度沿BC→CD方向運動,當P運動到B點時,P、Q兩點同時停止運動.設P點運動的時間為t,△APQ的面積為S,則S與t的函數關系的圖象是( )
A.
B.
C.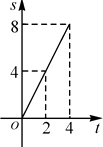
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c的圖象如圖所示,則下列結論:①abc<0,②b<a+c,③4a+2b+c>0,④2c<3b,⑤a+b<m(am+b)(m≠1)中正確的是( ) 
A.②④⑤
B.①②④
C.①③④
D.①③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小河上有一拱橋,拱橋及河道的截面輪廓線由拋物線的一部分ACB和矩形的三邊AE,ED,DB組成,已知河底ED是水平的,ED=16米,AE=8米,拋物線的頂點C到ED的距離是11米,以ED所在的直線為x軸,拋物線的對稱軸為y軸建立平面直角坐標系. 
(1)求拋物線的解析式;
(2)已知從某時刻開始的40小時內,水面與河底ED的距離h(單位:米)隨時間t(單位:時)的變化滿足函數關系h=﹣ ![]() (t﹣19)2+8(0≤t≤40),且當水面到頂點C的距離不大于5米時,需禁止船只通行,請通過計算說明:在這一時段內,需多少小時禁止船只通行?
(t﹣19)2+8(0≤t≤40),且當水面到頂點C的距離不大于5米時,需禁止船只通行,請通過計算說明:在這一時段內,需多少小時禁止船只通行?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一座拋物線形拱橋,校下面在正常水位時AB寬20米,水位上升3米就達到警戒線CD,這時水面寬度為10米. 
(1)在如圖的坐標系中,求拋物線的表達式;
(2)若洪水到來是水位以0.2米/時的速度上升,從正常水位開始,再過幾小時能到達橋面?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某中學組織學生進行“低碳生活”知識競賽,為了了解本次競賽的成績,把學生成績分成A、B、C、D、E五個等級,并繪制如圖的統計圖(不完整)統計成績.若扇形的半徑為2cm,則C等級所在的扇形的面積是cm2 . 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com