
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() (
(![]() 在
在![]() 的左側),與
的左側),與![]() 軸交于點
軸交于點![]() ,拋物線上的點
,拋物線上的點![]() 的橫坐標為3,過點
的橫坐標為3,過點![]() 作直線
作直線![]() 軸.
軸.
(1)點![]() 為拋物線上的動點,且在直線
為拋物線上的動點,且在直線![]() 的下方,點
的下方,點![]() ,
,![]() 分別為
分別為![]() 軸,直線
軸,直線![]() 上的動點,且
上的動點,且![]() 軸,當
軸,當![]() 面積最大時,求
面積最大時,求![]() 的最小值;
的最小值;
(2)過(1)中的點![]() 作
作![]() ,垂足為
,垂足為![]() ,且直線
,且直線![]() 與
與![]() 軸交于點
軸交于點![]() ,把
,把![]() 繞頂點
繞頂點![]() 旋轉45°,得到
旋轉45°,得到![]() ,再把
,再把![]() 沿直線
沿直線![]() 平移至
平移至![]() ,在平面上是否存在點
,在平面上是否存在點![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形為菱形?若存在直接寫出點
為頂點的四邊形為菱形?若存在直接寫出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
【答案】(1)![]() (2)
(2)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)根據題意求得點![]() 、
、![]() 、
、![]() 、
、![]() 的坐標,進而求得直線
的坐標,進而求得直線![]() 和直線
和直線![]() 解析式.過點
解析式.過點![]() 作
作![]() 軸垂線
軸垂線![]() 交
交![]() 于點
于點![]() ,設點
,設點![]() 橫坐標為
橫坐標為![]() ,即能用
,即能用![]() 表示
表示![]() 、
、![]() 的坐標進而表示
的坐標進而表示![]() 的長.由
的長.由![]() 得到關于
得到關于![]() 的二次函數,即求得
的二次函數,即求得![]() 為何值時
為何值時![]() 面積最大,求得此時點
面積最大,求得此時點![]() 坐標.把點
坐標.把點![]() 向上平移
向上平移![]() 的長,易證四邊形
的長,易證四邊形![]() 是平行四邊形,故有
是平行四邊形,故有![]() .在直線
.在直線![]() 的上方以
的上方以![]() 為斜邊作等腰
為斜邊作等腰![]() ,則有
,則有![]() .所以
.所以![]() ,其中
,其中![]() 的長為定值,易得當點
的長為定值,易得當點![]() 、
、![]() 、
、![]() 在同一直線上時,線段和的值最小.又點
在同一直線上時,線段和的值最小.又點![]() 是動點,
是動點,![]() ,由垂線段最短可知過點
,由垂線段最短可知過點![]() 作
作![]() 的垂線段
的垂線段![]() 時,
時,![]() 最短.求直線
最短.求直線![]() 、
、![]() 解析式,聯立方程組即求得點
解析式,聯立方程組即求得點![]() 坐標,進而求得
坐標,進而求得![]() 的長.
的長.
(2)先求得![]() ,
,![]() ,
,![]() 的坐標,可得
的坐標,可得![]() 是等腰直角三角形,當
是等腰直角三角形,當![]() 繞
繞![]() 逆時針旋轉
逆時針旋轉![]() 再沿直線
再沿直線![]() 平移可得△
平移可得△![]() ,根據以
,根據以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形為菱形,可得
為頂點的四邊形為菱形,可得![]() ,
,![]() ,
,![]() ,
,![]() ,即可求得
,即可求得![]() 的坐標,當
的坐標,當![]() 繞
繞![]() 順時針旋轉
順時針旋轉![]() 再沿直線
再沿直線![]() 平移可得△
平移可得△![]() ,根據以
,根據以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形為菱形,可得
為頂點的四邊形為菱形,可得![]() ,
,![]() ,即可求得
,即可求得![]() 的坐標.
的坐標.
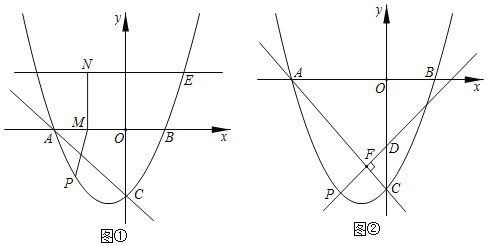
解:(1)如圖1,過點![]() 作
作![]() 軸于點
軸于點![]() ,交
,交![]() 于點
于點![]() ,在
,在![]() 上截取
上截取![]() ,連接
,連接![]() ,
,

以![]() 為斜邊在直線
為斜邊在直線![]() 上方作等腰
上方作等腰![]() ,過點
,過點![]() 作
作![]() 于點
于點![]()
![]() 時,
時,![]()
![]()
![]() 時,
時,![]()
解得:![]() ,
,![]()
![]() ,
,![]()
![]() 直線
直線![]() 解析式為
解析式為![]()
![]() 拋物線上的點
拋物線上的點![]() 的橫坐標為3
的橫坐標為3
![]()
![]() ,直線
,直線![]()
![]() 點
點![]() 在
在![]() 軸上,點
軸上,點![]() 在直線
在直線![]() 上,
上,![]() 軸
軸
![]()
設拋物線上的點![]() ,
,![]()
![]()
![]()
![]()
![]() 當
當![]() 時,
時,![]() 最大
最大
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
![]() 四邊形
四邊形![]() 是平行四邊形
是平行四邊形
![]()
![]() 等腰
等腰![]() 中,
中,![]() 為斜邊
為斜邊
![]() ,
,![]()
![]()
![]()
![]() 當點
當點![]() 、
、![]() 、
、![]() 在同一直線上時,
在同一直線上時,![]() 最小
最小
![]()
設直線![]() 解析式為
解析式為![]()
![]() 解得:
解得:![]()
![]() 直線
直線![]()
設直線![]() 解析式為
解析式為![]()
![]() 解得:
解得:![]()
![]() 直線
直線![]()
![]()
 解得:
解得:![]()
![]() ,
,![]()
![]()
![]() 最小值為
最小值為![]()
(2)![]() ,
,![]() ,
,
![]() 直線
直線![]() 解析式為:
解析式為:![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,
如圖2,把![]() 繞頂點
繞頂點![]() 逆時針旋轉
逆時針旋轉![]() ,得到△
,得到△![]() ,
,![]() ,
,![]() ,
,![]()
把△![]() 沿直線
沿直線![]() 平移至△
平移至△![]() ,連接
,連接![]() ,
,![]()

則直線![]() 解析式為
解析式為![]() ,直線
,直線![]() 解析式為
解析式為![]() ,顯然
,顯然![]()
![]() 以
以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形為菱形,
為頂點的四邊形為菱形,![]() 不可能為邊,只能以
不可能為邊,只能以![]() 、
、![]() 為鄰邊構成菱形
為鄰邊構成菱形
![]() ,
,
![]() ,
,![]()
![]()
![]() ,
,![]() ,
,
如圖3,把![]() 繞頂點
繞頂點![]() 順時針旋轉
順時針旋轉![]()


 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:初中數學 來源: 題型:
【題目】為做好食堂的服務工作,某學校食堂對學生最喜愛的菜肴進行了抽樣調查,下面試根據收集的數據繪制的統計圖(不完整):
(1)參加抽樣調查的學生數是______人,扇形統計圖中“大排”部分的圓心角是______°;
(2)把條形統計圖補充完整;
(3)若全校有3000名學生,請你根據以上數據估計最喜愛“烤腸”的學生人數.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,點D是△ABC內一點,AD=BD,且AD⊥BD,連接CD.過點C作CE⊥BC交AD的延長線于點 E,連接BE.過點D作DF⊥CD交BC于點F.
(1)若BD=DE= ![]() ,CE=
,CE= ![]() ,求BC的長;
,求BC的長;
(2)若BD=DE,求證:BF=CF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,反比例函數y1=![]() 與一次函數y2=mx+n相交于A(﹣1,2),B(4,a)兩點,AE⊥y軸于點E,則:
與一次函數y2=mx+n相交于A(﹣1,2),B(4,a)兩點,AE⊥y軸于點E,則:
(1)求反比例函數與一次函數的解析式;
(2)若y1≤y2則直接寫出x的取值范圍;
(3)若M為反比例函數上第四象限內的一個動點,若滿足S△ABM=S△AOB,則求點M的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=CB,∠ABC=90°,D為AB延長線上一點,點E在BC上,且BE=BD,連接AE、DE、DC.若∠CAE=30°,則∠BDC=_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某數學興趣小組同學進行測量大樹CD高度的綜合實踐活動,如圖,在點A處測得直立于地面的大樹頂端C的仰角為36°,然后沿在同一剖面的斜坡AB行走13米至坡頂B處,然后再沿水平方向行走6米至大樹腳底點D處,斜面AB的坡度(或坡比)i=1:2.4,那么大樹CD的高度約為(參考數據:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )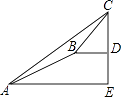
A.8.1米
B.17.2米
C.19.7米
D.25.5米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,∠ABC的平分線BE交CD于點E,∠ADC的平分線DF交AB于點F.
(1)若AD=4,AB=6,求BF的長.
(2)求證:四邊形DEBF是平行四邊形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小彬和爸爸一起去車站接從外地學習回來的媽媽,在去的過程中,小彬坐在汽車上看著時速表,用所學知識繪制了一張反映小車速度與時間的關系圖,請你根據圖象回答以下問題:

(1)在上述過程中,自變量是什么?因變量是什么?
(2)小車共行駛了多少時間?最高時速是多少?
(3)汽車在哪段時間保持勻速運動?速度是多少?
(4)汽車在哪段時間內速度在增加?哪段時間內速度在減少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,線段AB=6cm,動點P以2cm/s的速度從A﹣B﹣A在線段AB上運動,到達點A后,停止運動;動點Q以1cm/s的速度從B﹣A在線段AB上運動,到達點A后,停止運動.若動點P,Q同時出發,設點Q的運動時間是t(單位:s)時,兩個動點之間的距離為S(單位:cm),則能表示S與t的函數關系的是( )
![]()
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com