
【題目】如圖,拋物線y=ax2+bx+c(a≠0)與x軸交于A(﹣4,0),B(2,0),與y軸交于點C(0,2).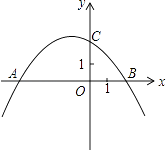
(1)求拋物線的解析式;
(2)若點D為該拋物線上的一個動點,且在直線AC上方,當以A、C、D為頂點的三角形面積最大時,求點D的坐標及此時三角形的面積;
(3)以AB為直徑作⊙M,直線經過點E(﹣1,﹣5),并且與⊙M相切,求該直線的解析式.
【答案】
(1)解:如圖1,
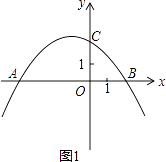
由題可得:
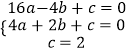 ,
,
解得: 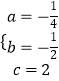 ,
,
∴拋物線的解析式為y=﹣ ![]() x2﹣
x2﹣ ![]() x+2;
x+2;
(2)解:過點D作DH⊥AB于H,交直線AC于點G,如圖2.
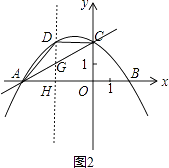
設直線AC的解析式為y=kx+t,
則有 ![]() ,
,
解得: ![]() ,
,
∴直線AC的解析式為y= ![]() x+2.
x+2.
設點D的橫坐標為m,則點G的橫坐標也為m,
∴DH=﹣ ![]() m2﹣
m2﹣ ![]() m+2,GH=
m+2,GH= ![]() m+2,
m+2,
∴DG=﹣ ![]() m2﹣
m2﹣ ![]() m+2﹣
m+2﹣ ![]() m﹣2=﹣
m﹣2=﹣ ![]() m2﹣m,
m2﹣m,
∴S△ADC=S△ADG+S△CDG
= ![]() DGAH+
DGAH+ ![]() DGOH=
DGOH= ![]() DGAO=2DG
DGAO=2DG
=﹣ ![]() m2﹣2m=﹣
m2﹣2m=﹣ ![]() (m2+4m)
(m2+4m)
=﹣ ![]() (m2+4m+4﹣4)
(m2+4m+4﹣4)
=﹣ ![]() [(m+2)2﹣4]
[(m+2)2﹣4]
=﹣ ![]() (m+2)2+2.
(m+2)2+2.
∴當m=﹣2時,S△ADC取到最大值2.
此時yD=﹣ ![]() ×(﹣2)2﹣
×(﹣2)2﹣ ![]() ×(﹣2)+2=2,
×(﹣2)+2=2,
即點D的坐標為(﹣2,2);
(3)解:設過點E的直線與⊙M相切于點F,與x軸交于點N,連接MF,如圖3,
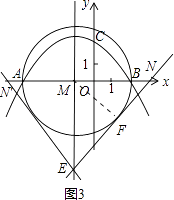
則有MF⊥EN.
∵A(﹣4,0),B(2,0),
∴AB=6,MF=MB=MA=3,
∴點M的坐標為(﹣4+3,0)即M(﹣1,0).
∵E(﹣1,﹣5),∴ME=5,∠EMN=90°.
在Rt△MFE中,EF= ![]() =
= ![]() =4.
=4.
∵∠MEF=∠NEM,∠MFE=∠EMN=90°,
∴△MEF∽△NEM,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴NM= ![]() ,
,
∴點N的坐標為(﹣1+ ![]() ,0)即(
,0)即( ![]() ,0)或(﹣1﹣
,0)或(﹣1﹣ ![]() ,0)即(﹣
,0)即(﹣ ![]() ,0).
,0).
設直線EN的解析式為y=px+q.
①當點N的坐標為( ![]() ,0)時,
,0)時,
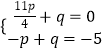 ,
,
解得: 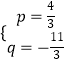 ,
,
∴直線EN的解析式為y= ![]() x﹣
x﹣ ![]() .
.
②當點N的坐標為(﹣ ![]() ,0)時,
,0)時,
同理可得:直線EN的解析式為y=﹣ ![]() x﹣
x﹣ ![]() .
.
綜上所述:所求直線的解析式為y= ![]() x﹣
x﹣ ![]() 或y=﹣
或y=﹣ ![]() x﹣
x﹣ ![]() .
.
【解析】(1)將已知三點的坐標代入拋物線的解析式可得到關于a、b、c的方程組,從而可求得a、b、c的值;
(2)過點D作DH⊥AB,垂足為H,交直線AC于點G,然后再求得AC的解析式,設點D的橫坐標為m,則點G的橫坐標也為m,從而可以用m的代數式表示出DG,然后用割補法得到△ADC的面積是關于m的二次函數,最后依據二次函數的最值即可;
(3)設過點E的直線與⊙M相切于點F,與x軸交于點N,連接MF,由切線的性質可知:MF⊥EN.然后再求得點M的坐標以及線段ME、MF、EF的長,接下來,再證明△MEF∽△NEM,然后依據相似三角形的性質可求出MN的長度,從而得到點N的坐標,最后,再運用待定系數法求解即可.


 一線名師提優(yōu)試卷系列答案
一線名師提優(yōu)試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠A=30°,BC=2 ![]() ,以直角邊AC為直徑作⊙O交AB于點D,則圖中陰影部分的面積是( )
,以直角邊AC為直徑作⊙O交AB于點D,則圖中陰影部分的面積是( )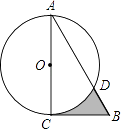
A.![]() ﹣
﹣ ![]()
B.![]() ﹣
﹣ ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某鞋店銷售了9雙鞋,各種尺碼的銷售量如下:
鞋的尺碼 | 20 | 21 | 22 | 23 |
銷售量(雙) | 1 | 2 | 4 | 2 |
(1)計算這9雙鞋尺碼的平均數、中位數和眾數.
(2)哪一個指標是鞋廠最感興趣的指標?哪一個指標是鞋廠最不感興趣的?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知平行四邊形ABCD中,CE平分∠BCD且交AD于點E,AF∥CE,且交BC于點F.
(1)求證:△ABF≌△CDE;
(2)如圖,若∠1=65°,求∠B的大小.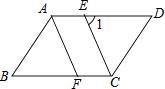
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC和△DEF都是等腰直角三角形,∠BAC=∠EDF=90°,△DEF的頂點E與△ABC的斜邊BC的中點重合.將△DEF繞點E旋轉,旋轉過程中,線段DE與線段AB相交于點P,射線EF與線段AB相交于點G,與射線CA相交于點Q.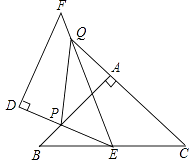
(1)求證:△BPE∽△CEQ;
(2)求證:DP平分∠BPQ;
(3)當BP=a,CQ= ![]() a,求PQ長(用含a的代數式表示).
a,求PQ長(用含a的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學的1號教學大樓共有4道門,其中兩道正門大小相同,兩道側門也大小相同,安全檢查時,對4道門進行了測試,當同時開啟一道正門和兩道側門時,2分鐘內可以通過560名學生,當同時開啟一道正門和一道側門時,4分鐘內可通過800名學生.
(1)求平均每分鐘一道正門和一道側門各可以通過多少名學生?
(2)該中學的2號教學大樓,有和1號教學大樓相同的正門和側門共5道,若這棟大樓的教室里最多有1920名學生,安全檢查規(guī)定,在緊急情況下,全大樓學生應在4分鐘內通過這5道門安全撤離,該棟大樓正門和側門各有幾道?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成下面推理過程
如圖,EF∥AD,∠1=∠2,∠BAC=70°.將求∠AGD的過程填寫完整.
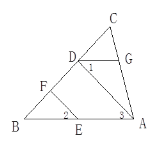
解: 因為EF∥AD,
所以∠2=____ (_________________________________)
又因為∠1=∠2
所以∠1=∠3 (__________________)
所以AB∥_____ (___________________________________)
所以∠BAC+______=180°(___________________________)
因為∠BAC=70°
所以∠AGD=_______.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com