
【題目】如圖,已知點A(0,4),B(2,0).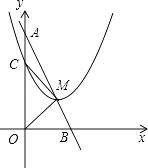
(1)求直線AB的函數解析式;
(2)已知點M是線段AB上一動點(不與點A、B重合),以M為頂點的拋物線y=(x﹣m)2+n與線段OA交于點C.
①求線段AC的長;(用含m的式子表示)
②是否存在某一時刻,使得△ACM與△AMO相似?若存在,求出此時m的值.
【答案】
(1)
解:設直線AB的函數解析式為:y=kx+b.
∵點A坐標為(0,4),點B坐標為(2,0),
∴ ![]() ,解得:
,解得: ![]() ,
,
即直線AB的函數解析式為y=﹣2x+4
(2)
解:①∵以M為頂點的拋物線為y=(x﹣m)2+n,
∴拋物線頂點M的坐標為(m,n).
∵點M在線段AB上,∴n=﹣2m+4,
∴y=(x﹣m)2﹣2m+4.
把x=0代入y=(x﹣m)2﹣2m+4,
得y=m2﹣2m+4,即C點坐標為(0,m2﹣2m+4),
∴AC=OA﹣OC=4﹣(m2﹣2m+4)=﹣m2+2m;
②存在某一時刻,能夠使得△ACM與△AMO相似.理由如下:
過點M作MD⊥y軸于點D,則D點坐標為(0,﹣2m+4),
∴AD=OA﹣OD=4﹣(﹣2m+4)=2m.
∵M不與點A、B重合,∴0<m<2,
又∵MD=m,∴AM= ![]() =
= ![]() m.
m.
∵在△ACM與△AMO中,∠CAM=∠MAO,∠MCA>∠AOM,
∴當△ACM與△AMO相似時,假設△ACM∽△AMO,
∴ ![]() ,即
,即 ![]() ,
,
整理,得 9m2﹣8m=0,解得m= ![]() 或m=0(舍去),
或m=0(舍去),
∴存在一時刻使得△ACM與△AMO相似,且此時m= ![]() .
.
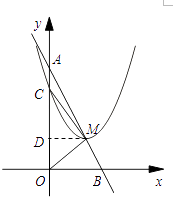
【解析】(1)設直線AB的函數解析式為:y=kx+b,將A、B兩點的坐標代入,運用待定系數法即可求出直線AB的函數解析式;(2)①先由拋物線的頂點式為y=(x﹣m)2+n得出頂點M的坐標為(m,n),由點M是線段AB上一動點,得出n=﹣2m+4,則y=(x﹣m)2﹣2m+4,再求出拋物線y=(x﹣m)2+n與y軸交點C的坐標,然后根據AC=OA﹣OC即可求解;②過點M作MD⊥y軸于點D,則D點坐標為(0,﹣2m+4),AD=OA﹣OD=2m,由勾股定理求出AM= ![]() m.在△ACM與△AMO中,由于∠CAM=∠MAO,∠MCA>∠AOM,所以當△ACM與△AMO相似時,只能是△ACM∽△AMO,根據相似三角形對應邊成比例得出
m.在△ACM與△AMO中,由于∠CAM=∠MAO,∠MCA>∠AOM,所以當△ACM與△AMO相似時,只能是△ACM∽△AMO,根據相似三角形對應邊成比例得出 ![]() ,即
,即 ![]() ,解方程求出m的值即可.
,解方程求出m的值即可.
【考點精析】本題主要考查了二次函數的性質的相關知識點,需要掌握增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小才能正確解答此題.


科目:初中數學 來源: 題型:
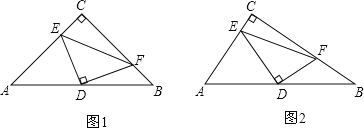
【題目】已知:如圖1,Rt△ABC中,∠ACB=90°,D為AB中點,DE、DF分別交AC于E,交BC于F,且DE⊥DF.
(1)如果CA=CB,求證:AE2+BF2=EF2;
(2)如圖2,如果CA<CB,(1)中結論還能成立嗎?若成立,請證明;若不成立,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題為真命題的是
A.有兩邊及一角對應相等的兩個三角形全等
B.方程x2+2x+3=0有兩個不相等的實數根
C.面積之比為1∶2的兩個相似三角形的周長之比是1∶4
D.順次連接任意四邊形各邊中點得到的四邊形是平行四邊形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,BC=6,分別以點A和點C為圓心,以相同的長(大于 ![]() AC)為半徑作弧,兩弧相交于點M和點N , 作直線MN交AB于點D , 交AC于點E , 連接CD . 則DE的長為 .
AC)為半徑作弧,兩弧相交于點M和點N , 作直線MN交AB于點D , 交AC于點E , 連接CD . 則DE的長為 . 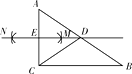
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜邊AB的垂直平分線交AC于點D,點F在AC上,點E在BC的延長線上,CE=CF,連接BF,DE.線段DE和BF在數量和位置上有什么關系?并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】初中生在數學運算中使用計算器的現象越來越普遍,某校一興趣小組隨機抽查了本校若干名學生使用計算器的情況.以下是根據抽查結果繪制出的不完整的條形統計圖和扇形統計圖: 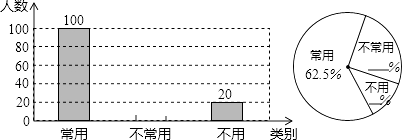
請根據上述統計圖提供的信息,完成下列問題:
(1)這次抽查的樣本容量是;
(2)請補全上述條形統計圖和扇形統計圖;
(3)若從這次接受調查的學生中,隨機抽查一名學生恰好是“不常用”計算器的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】應用探究題 在圖①中,已知長方形的長和寬分別為a,b,將線段A1A2向右平移1個單位長度到B1B2的位置,得到封閉圖形A1A2B2B1(即陰影部分).
在圖②中,將折線A1A2A3向右平移1個單位長度到折線B1B2B3的位置,得到封閉圖形A1A2A3B3B2B1(即陰影部分).
(1)在圖③中,請你畫一條類似的有兩個折點的折線,同樣向右平移1個單位長度,從而得到一個封閉圖形,并用陰影表示;
(2)請你分別寫出前三個圖形中除去陰影部分后剩余部分的面積:S1,S2,S3;
(3)聯想與探索:
如圖④,在一塊長方形草地上,草地的長和寬仍分別為a,b,有一條彎曲的柏油小路(小路任何地方的水平寬度都是1個單位長度),請你猜想空白部分表示的草地面積是多少,并說明你的猜想是正確的.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com