
【題目】閱讀下列材料,并解爺其后的問題:
我們知道,三角形的中位線平行于第一邊,且等于第三邊的一半,我們還知道,三角形的三條中位線可以將三角形分成四個全等的一角形,如圖1,若D、E、F分別是![]() 三邊的中點,則有
三邊的中點,則有![]() ,且
,且![]()



(1)在圖1中,若![]() 的面積為15,則
的面積為15,則![]() 的面積為___________;
的面積為___________;
(2)在圖2中,已知E、F、G、H分別是AB、BC、CD、AD的中點,求證:四邊形EFGH是平行四邊形;
(3)如圖3中,已知E、F、G、H分別是AB、BC、CD、AD的中點,![]() ,則四邊形EFGH的面積為___________.
,則四邊形EFGH的面積為___________.
【答案】(1)![]() ;(2)見解析;(3)5.
;(2)見解析;(3)5.
【解析】
(1)由三角形中位線定理得出DF∥BC,且DF=![]() BC,△ADF≌△DBE≌△FEC≌△EFD,得出△DEF的面積=
BC,△ADF≌△DBE≌△FEC≌△EFD,得出△DEF的面積=![]() △ABC的面積=
△ABC的面積=![]() 即可;
即可;
(2)連接BD,證出EH是△ABD的中位線,FG是△BCD的中位線,由三角形中位線定理得出EH∥BD,EH=![]() BD,FG∥BD,FG=
BD,FG∥BD,FG=![]() BD,得出EH∥FG,EH=FG,即可得出結論;
BD,得出EH∥FG,EH=FG,即可得出結論;
(3)證出EH是△ABD的中位線,FG是△BCD的中位線,由三角形中位線定理得出EH∥BD,EH=![]() BD=
BD=![]() ,FG∥BD,FG=
,FG∥BD,FG=![]() BD,得出EH∥FG,EH=FG,證出四邊形EFGH是平行四邊形,同理:EF∥AC,EF=
BD,得出EH∥FG,EH=FG,證出四邊形EFGH是平行四邊形,同理:EF∥AC,EF=![]() AC=2,證出EH⊥EF,得出四邊形EFGH是矩形,即可得出結果.
AC=2,證出EH⊥EF,得出四邊形EFGH是矩形,即可得出結果.
(1)解:∵D、E、F分別是△ABC三邊的中點,
則有DF∥BC,且DF=![]() BC,△ADF≌△DBE≌△FEC≌△EFD,
BC,△ADF≌△DBE≌△FEC≌△EFD,
∴△DEF的面積=![]() △ABC的面積=
△ABC的面積=![]() ;
;
故答案為:![]() ;
;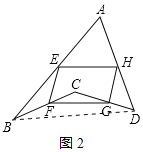
(2)證明:連接BD,如圖2所示:
∵E、F、G、H分別是AB、BC、CD、AD的中點,
∴EH是△ABD的中位線,FG是△BCD的中位線,
∴EH∥BD,EH=![]() BD,FG∥BD,FG=
BD,FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四邊形EFGH是平行四邊形;
(3)解:∵E、F、G、H分別是AB、BC、CD、AD的中點,
∴EH是△ABD的中位線,FG是△BCD的中位線,
∴EH∥BD,EH=![]() BD=
BD=![]() ,FG∥BD,FG=
,FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四邊形EFGH是平行四邊形,
同理:EF∥AC,EF=![]() AC=2,
AC=2,
∵AC⊥BD,
∴EH⊥EF,
∴四邊形EFGH是矩形,
∴四邊形EFGH的面積=EH×EF=![]() ×2=5.
×2=5.
故答案為:(1)![]() ;(2)見解析;(3)5.
;(2)見解析;(3)5.


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=6,AD=8,以BC為斜邊在矩形的外部作直角三角形BEC,點F是CD的中點,則EF的最大值為( )
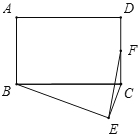
A. 8B. 9C. 10D. 2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分9分)如圖,以⊿ABC的一邊AB為直徑的半圓與其它兩邊AC,BC的交點分別為D,E,且![]() .
.
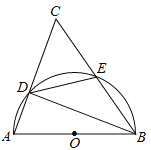
(1)試判斷⊿ABC的形狀,并說明理由;
(2)已知半圓的半徑為5,BC=12,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中描出下列各組點,并將各組的點用線段依次連結起來.
(1)(1,0)、(6,0)、(6,1)、(5,0)、(6,-1)、(6,0);
(2)(2,0)、(5,3)、(4,0);
(3)(2,0)、(5,-3)、(4,0).
觀察所得到的圖形像什么?如果要將此圖形向上平移到x軸上方,那么至少要向上平移幾個單位長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某九年級制學校圍繞“每天30分鐘的大課間,你最喜歡的體育活動項目是什么?(只寫一項)”的問題,對在校學生進行隨機抽樣調查,從而得到一組數據.圖1是根據這組數據繪制的條形統計圖,請結合統計圖回答下列問題:

(1)該校對多少學生進行了抽樣調查?
(2)本次抽樣調查中,最喜歡籃球活動的有多少?占被調查人數的百分比是多少?
(3)若該校九年級共有200名學生,圖2是根據各年級學生人數占全校學生總人數的百分比繪制的扇形統計圖,請你估計全校學生中最喜歡跳繩活動的人數約為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】長方體敞口玻璃罐,長、寬、高分別為16 cm、6 cm和6 cm,在罐內點E處有一小塊餅干碎末,此時一只螞蟻正好在罐外壁,在長方形ABCD中心的正上方2 cm處,則螞蟻到達餅干的最短距離是多少cm.( )
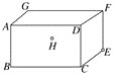
A. 7![]() B.
B. ![]()
C. 24D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市“健益”超市購進一批![]() 元/千克的綠色食品,如果以
元/千克的綠色食品,如果以![]() 元/千克銷售,那么每天可售出
元/千克銷售,那么每天可售出![]() 千克.由銷售經驗知,每天銷售量
千克.由銷售經驗知,每天銷售量![]() (千克)與銷售單價
(千克)與銷售單價![]() (元)(
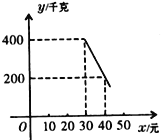
(元)(![]() )存在如下圖所示的一次函數關系.
)存在如下圖所示的一次函數關系.
(1)試求出y與x的函數關系式;
(2)設“健益”超市銷售該綠色食品每天獲得利潤p元,當銷售單價為何值時,每天可獲得 最大利潤?最大利潤是多少?
(3)根據市場調查,該綠色食品每天可獲利潤不超過4480元,現該超市經理要求每天利潤不得低于4180元,請你幫助該超市確定綠色食品銷售單價x的范圍(直接寫出).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com