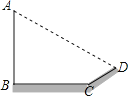
【題目】如圖，某天小明發現陽光下電線桿AB的影子落在土坡的坡面CD和地面BC上，量的CD=8米，BC=20米，斜坡CD的坡度比為1：
，且此時測得1米桿的影長為2米，則電線桿的高度為（ ）
A．（14+2
）米 B．28米 C．（7+）米 D．9米
【答案】A
【解析】
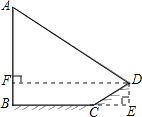
試題分析：根據已知條件，過D分別作BC、AB的垂線，設垂足為E、F；在Rt△DCE中，已知斜邊CD的長和斜坡CD的坡度比為1：
，得出∠DCE的度數，滿足解直角三角形的條件，可求出DE、CE的長．即可求得DF、BF的長；在Rt△ADF中，已知了“1米桿的影長為2米”，即坡面AD的坡度為
，根據DF的長，即可求得AF的長，AB=AF+BF．
解：如圖所示：過D作DE垂直BC的延長線于E，且過D作DF⊥AB于F，
∵在Rt△DEC中，CD=8，斜坡CD的坡度比為1：，
∴∠DCE=30°，
∴DE=4米，CE=4米，
∴BF=4米，DF=20+4（米），
∵1米桿的影長為2米，
∴
=，
則AF=（10+2）米，
AB=AF+BF=10+2
+4=（14+2）米，
∴電線桿的高度（14+2）米．
故選：A．
科目：初中數學 來源： 題型：
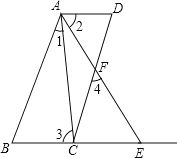
【題目】如圖AB∥CD．∠1=∠2，∠3=∠4，試說明AD∥BE．
解：∵AB∥CD（已知）
∴∠4=∠ （ ）
∵∠3=∠4（已知）
∴∠3=∠ （ ）
∵∠1=∠2（已知）
∴∠1+∠CAF=∠2+∠CAF（
即∠ =∠ （ ）
∴∠3=∠
∴AD∥BE（ ）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】作圖題：
（1）如圖，在圖1所給方格紙中，每個小正方形邊長都是1，標號為①②③的三個三角形均為格點三角形（頂點在方格頂點處），請按要求將圖2中的指定圖形分割成三個三角形，使它們與標號為①②③的三個三角形分別對應全等．（分割線畫成實線）
（2）如圖3，在長度為1個單位長度的小正方形組成的正方形網格中，點A、B、C在小正方形的頂點上．
①在圖中畫出與△ABC關于直線L成軸對稱的△A′B′C′；
②請直線L上找到一點P，使得PC+PB的距離之和最小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，Rt△ABC中，∠ABC=90°，以AB為直徑作半圓⊙O交AC與點D，點E為BC的中點，連接DE．
（1）求證：DE是半圓⊙O的切線．
（2）若∠BAC=30°，DE=2，求AD的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】實驗學校九年級一班十名同學定點投籃測試，每人投籃六次，投中的次數統計如下：5，4，3，5，5，2，5，3，4，1，則這組數據的中位數，眾數分別為（ ）
A. 4，5 B. 5，4 C. 4，4 D. 5，5
查看答案和解析>>
科目：初中數學 來源： 題型：
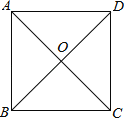
【題目】如圖，四邊形ABCD是正方形，對角線AC，BD交于點O，下列結論：①OA=OB；②∠ACB=45°；③AC⊥BD；④正方形ABCD有四條對稱軸．上述結論正確的有（ ）
A．①②③④ B．①②③ C．②③④ D．①③④
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若關于x的一元二次方程kx2﹣2x﹣1=0有兩個不相等的實數根，則k的取值范圍是（ ）
A．k＞﹣1 B．k＞﹣1且k≠0 C．k＜1 D．k＜1且k≠0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com